Los números primos hasta el número 20 son 2,3,5,7,11,13,17 y 19.
¿Cómo sabemos si un número es divisible por un número primo?
Aquí os dejo las reglas de divisibilidad de los primeros números primos.
Números divisibles entre 2 todos los números pares.
Ejemplos: 8,24,36
Números divisibles entre 3 los números cuyas todas cifras suman un número múltiplo de 3.
Ejemplos: 6, 21 ( 2+1=3), 54 (5+4=9) 9 múltiplo de 3
Números divisibles entre 5 los números cuya unidad acaba en 0 ó 5.
Ejemplos: 10, 35, 1000, 11115.
Números divisibles entre 7 son aquellos que eliminando la unidad y restando el doble de la unidad es un 0 ó múltiplo de 7.
Ejemplo: 371 (37-2·1=35) 35 es múltiplo de 7.
Números divisibles entre 11 son aquellos que si la diferencia de la suma de cifras de posición par e impar es 0 o múltiplo de 11.
Ejemplo: 275 Impares 2+5=7 Pares 7 Impares -Pares = 7-7 = 0.
En los números que terminan en 0 es más fácil factorizarlos como 2·5.
Aquí os dejo unos ejercicios resueltos de descomposición en factores primos.
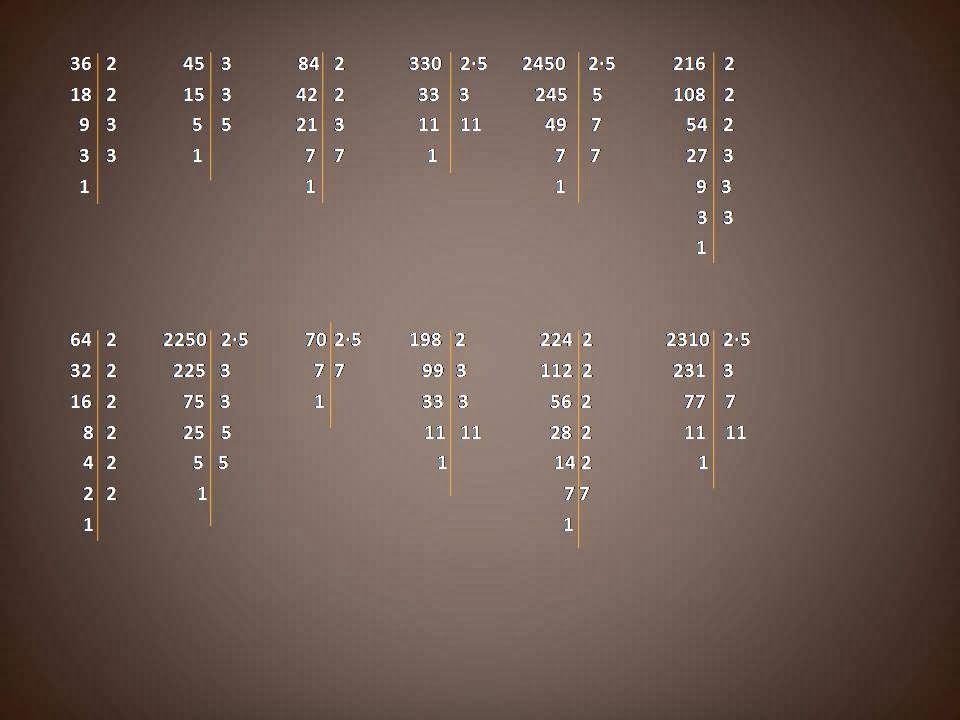height="480" width="640" />Por lo tanto:
\(36=2^{2}\cdot 3^{2}\)
\(45=3^{2}\cdot 5\)
\(84=2^{2}\cdot 3\cdot 7\)
\(330=2\cdot 3\cdot 5\cdot 11\)
\(2450=2\cdot 5^{2}\cdot 7^{2}\)
\(216=2^{3}\cdot 3^{3}\)
\(64=2^{6}\)
\(2250=2\cdot 3^{2}\cdot 5^{3}\)
\(70=2\cdot 5\cdot 7\)
\(198=2\cdot 3^{2}\cdot 11\)
\(224=2^{5}\cdot 7\)
\(2310=2\cdot 5\cdot 3\cdot 7\cdot 11\)
0 comentarios:
Publicar un comentario