Dos ángulos son complementarios cuando la suma de ambos es 90º.
Para hallar el angulo complementario de un ángulo será necesario restar a 90º el ángulo dado.
Ejemplos:
\(\bullet\) Hallar el ángulo complementario de \(23^{\circ}\ 22'\ 43''\)
\[\begin{array}{rrr} 90^{\circ} & \color{white}{0} & \color{white}{0} \\ -23^{\circ} & 22' & 43'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 89^{\circ} & 60' & \color{white}{0} \\ -23^{\circ} & 22' & 43'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 89^{\circ} & 59' & 60'' \\ -23^{\circ} & 22' & 43'' \\ \hline \\ 66^{\circ} & 37' & 17''\end{array}\]
\(\bullet\) Hallar el ángulo complementario de \(47^{\circ}\ 50'\ 5''\)
\[\begin{array}{rrr} 90^{\circ} & \color{white}{0} & \color{white}{0} \\ -47^{\circ} & 50' & 5'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 89^{\circ} & 60' & \color{white}{0} \\ -47^{\circ} & 50' & 5'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 89^{\circ} & 59' & 60'' \\ -47^{\circ} & 50' & 5'' \\ \hline \\ 42^{\circ} & 9' & 55''\end{array}\]
\(\bullet\) Hallar el ángulo complementario de \(1^{\circ}\ 2'\ 33''\)
\[\begin{array}{rrr} 90^{\circ} & \color{white}{0} & \color{white}{0} \\ -1^{\circ} & 2' & 33'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 89^{\circ} & 60' & \color{white}{0} \\ -1^{\circ} & 22' & 33'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 89^{\circ} & 59' & 60'' \\ -1^{\circ} & 2' & 33'' \\ \hline \\ 88^{\circ} & 57' & 27''\end{array}\]
\(\bullet\) Hallar el ángulo complementario de \(83^{\circ}\ 4'\ 27''\)
\[\begin{array}{rrr} 90^{\circ} & \color{white}{0} & \color{white}{0} \\ -83^{\circ} & 4' & 27'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 89^{\circ} & 60' & \color{white}{0} \\ -83^{\circ} & 4' & 27'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 89^{\circ} & 59' & 60'' \\ -83^{\circ} & 4' & 27'' \\ \hline \\ 6^{\circ} & 55' & 33''\end{array}\]
Ya es todo, seguid practicando
viernes, 28 de febrero de 2014
/>Ángulos suplementarios
Dos ángulos son suplementarios cuando la suma de ambos son 180º.
Para hallar el ángulo suplementario de otro es necesario restar a 180º el ángulo dado.
Aquí os dejo unos ejercicios:
\(\bullet\) Hallar el ángulo complementario de \(32^{\circ}\ 58'\ 41''\)
\[\begin{array}{rrr} 180^{\circ} & \color{white}{0} & \color{white}{0} \\ -32^{\circ} & 58' & 41'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 60' & \color{white}{0} \\ -32^{\circ} & 58' & 41'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 59' & 60'' \\ -32^{\circ} & 58' & 41'' \\ \hline \\ 147^{\circ} & 1' & 19''\end{array}\]
\(\bullet\) Hallar el ángulo complementario de \(122^{\circ}\ 11'\ 41''\)
\[\begin{array}{rrr} 180^{\circ} & \color{white}{0} & \color{white}{0} \\ -122^{\circ} & 11' & 41'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 60' & \color{white}{0} \\ -122^{\circ} & 11' & 41'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 59' & 60'' \\ -122^{\circ} & 11' & 41'' \\ \hline \\ 57^{\circ} & 48' & 19''\end{array}\]
\(\bullet\) Hallar el ángulo complementario de \(43^{\circ}\ 10'\ 29''\)
\[\begin{array}{rrr} 180^{\circ} & \color{white}{0} & \color{white}{0} \\ -43^{\circ} & 10' & 29'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 60' & \color{white}{0} \\ -43^{\circ} & 10' & 29'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 59' & 60'' \\ -43^{\circ} & 10' & 29'' \\ \hline \\ 136^{\circ} & 49' & 31''\end{array}\]
\(\bullet\) Hallar el ángulo complementario de \(5^{\circ}\ 17''\)
\[\begin{array}{rrr} 180^{\circ} & \color{white}{0} & \color{white}{0} \\ -5^{\circ} & \color{white}{0} & 17'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 60' & \color{white}{0} \\ -5^{\circ} & \color{white}{0} & 17'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 59' & 60'' \\ -5^{\circ} & \color{white}{0} & 17'' \\ \hline \\ 174^{\circ} & 59' & 43''\end{array}\]
Si tenéis alguna duda sobre los ejercicios, dejadme un post. Gracias
Para hallar el ángulo suplementario de otro es necesario restar a 180º el ángulo dado.
/>Aquí os dejo unos ejercicios:
\(\bullet\) Hallar el ángulo complementario de \(32^{\circ}\ 58'\ 41''\)
\[\begin{array}{rrr} 180^{\circ} & \color{white}{0} & \color{white}{0} \\ -32^{\circ} & 58' & 41'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 60' & \color{white}{0} \\ -32^{\circ} & 58' & 41'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 59' & 60'' \\ -32^{\circ} & 58' & 41'' \\ \hline \\ 147^{\circ} & 1' & 19''\end{array}\]
\(\bullet\) Hallar el ángulo complementario de \(122^{\circ}\ 11'\ 41''\)
\[\begin{array}{rrr} 180^{\circ} & \color{white}{0} & \color{white}{0} \\ -122^{\circ} & 11' & 41'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 60' & \color{white}{0} \\ -122^{\circ} & 11' & 41'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 59' & 60'' \\ -122^{\circ} & 11' & 41'' \\ \hline \\ 57^{\circ} & 48' & 19''\end{array}\]
\(\bullet\) Hallar el ángulo complementario de \(43^{\circ}\ 10'\ 29''\)
\[\begin{array}{rrr} 180^{\circ} & \color{white}{0} & \color{white}{0} \\ -43^{\circ} & 10' & 29'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 60' & \color{white}{0} \\ -43^{\circ} & 10' & 29'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 59' & 60'' \\ -43^{\circ} & 10' & 29'' \\ \hline \\ 136^{\circ} & 49' & 31''\end{array}\]
\(\bullet\) Hallar el ángulo complementario de \(5^{\circ}\ 17''\)
\[\begin{array}{rrr} 180^{\circ} & \color{white}{0} & \color{white}{0} \\ -5^{\circ} & \color{white}{0} & 17'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 60' & \color{white}{0} \\ -5^{\circ} & \color{white}{0} & 17'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 179^{\circ} & 59' & 60'' \\ -5^{\circ} & \color{white}{0} & 17'' \\ \hline \\ 174^{\circ} & 59' & 43''\end{array}\]
Si tenéis alguna duda sobre los ejercicios, dejadme un post. Gracias
Sistema sexagesimal. Resta de ángulos
Para restar ángulos tenemos que hacer como en la suma. Restaremos los grados con los grados, los minutos con los minutos y los segundos con los segundos.
El problema viene cuando en los minutos y los segundos del ángulo que resta es mayor. Lo que tenemos que hacer es añadir un grado a los minutos (60 minutos) y/o añadir un minuto a los segundos (60 segundos).
En los siguientes ejercicios vamos a ver todos los casos.
\(\bullet 45^{\circ}\ 25'\ 30''\ - \ 20^{\circ}\ 15'\ 5''\ \)
\[\begin{array}{rrr} 45^{\circ} & 25' & 30'' \\ -20^{\circ} & 15' & 5'' \\ \hline \\ 25^{\circ} & 10' & 25''\end{array}\]
\(\bullet 25^{\circ}\ 15'\ 30''\ - \ 12^{\circ}\ 20'\ 25''\ \)
\[\begin{array}{rrr} 25^{\circ} & 15' & 30'' \\ -12^{\circ} & 20' & 25'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 24^{\circ} & 75' & 30'' \\ -12^{\circ} & 20' & 25'' \\ \hline \\ 12^{\circ} & 55' & 5''\end{array}\]
\(\bullet 52^{\circ}\ 27'\ 15''\ - \ 23^{\circ}\ 15'\ 42''\ \)
\[\begin{array}{rrr} 52^{\circ} & 27' & 15'' \\ -23^{\circ} & 15' & 42'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 52^{\circ} & 26' & 75'' \\ -23^{\circ} & 15' & 42'' \\ \hline \\ 29^{\circ} & 11' & 13''\end{array}\]
\(\bullet 25^{\circ}\ 37'\ 25''\ - \ 12^{\circ}\ 43'\ 55''\ \)
\[\begin{array}{rrr} 25^{\circ} & 37' & 25'' \\ -12^{\circ} & 43' & 55'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 24^{\circ} & 97' & 25'' \\ -12^{\circ} & 43' & 55'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 24^{\circ} & 96' & 85'' \\ -12^{\circ} & 43' & 55'' \\ \hline \\ 12^{\circ} & 53' & 30''\end{array}\]
Bueno si tenéis alguna pregunta o sobre cualquier ejercicio de matemáticas, no olvidéis en poner un post. Muchas gracias
El problema viene cuando en los minutos y los segundos del ángulo que resta es mayor. Lo que tenemos que hacer es añadir un grado a los minutos (60 minutos) y/o añadir un minuto a los segundos (60 segundos).
En los siguientes ejercicios vamos a ver todos los casos.
\(\bullet 45^{\circ}\ 25'\ 30''\ - \ 20^{\circ}\ 15'\ 5''\ \)
\[\begin{array}{rrr} 45^{\circ} & 25' & 30'' \\ -20^{\circ} & 15' & 5'' \\ \hline \\ 25^{\circ} & 10' & 25''\end{array}\]
\(\bullet 25^{\circ}\ 15'\ 30''\ - \ 12^{\circ}\ 20'\ 25''\ \)
\[\begin{array}{rrr} 25^{\circ} & 15' & 30'' \\ -12^{\circ} & 20' & 25'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 24^{\circ} & 75' & 30'' \\ -12^{\circ} & 20' & 25'' \\ \hline \\ 12^{\circ} & 55' & 5''\end{array}\]
\(\bullet 52^{\circ}\ 27'\ 15''\ - \ 23^{\circ}\ 15'\ 42''\ \)
\[\begin{array}{rrr} 52^{\circ} & 27' & 15'' \\ -23^{\circ} & 15' & 42'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 52^{\circ} & 26' & 75'' \\ -23^{\circ} & 15' & 42'' \\ \hline \\ 29^{\circ} & 11' & 13''\end{array}\]
\(\bullet 25^{\circ}\ 37'\ 25''\ - \ 12^{\circ}\ 43'\ 55''\ \)
\[\begin{array}{rrr} 25^{\circ} & 37' & 25'' \\ -12^{\circ} & 43' & 55'' \\ \hline \\ \color{white}{0} & & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 24^{\circ} & 97' & 25'' \\ -12^{\circ} & 43' & 55'' \\ \hline \\ \color{white}{0} & \color{white}{0} & \color{white}{0}\end{array}\rightarrow\begin{array}{rrr} 24^{\circ} & 96' & 85'' \\ -12^{\circ} & 43' & 55'' \\ \hline \\ 12^{\circ} & 53' & 30''\end{array}\]
Bueno si tenéis alguna pregunta o sobre cualquier ejercicio de matemáticas, no olvidéis en poner un post. Muchas gracias
jueves, 27 de febrero de 2014
Suma de ángulos en forma compleja
La suma de ángulos en forma compleja es sencilla. Sumamos grados con grados, minutos con minutos y segundos con segundos. El problema viene cuando los minutos o segundos suman más de 60.
Lo que tenemos que hacer es restar 60 a los minutos, (si es mayor de 60 el número de minutos) y sumar 1 grado. Si son los segundos los que suman más de 60 sumamos un minuto y restamos 60 segundos.
Lo vamos a ver más fácil con unos ejemplos.
\(\bullet 45^{\circ}\ 23'\ 15''\ + \ 23^{\circ}\ 32'\ 24''\ \)
\[\begin{array}{rrr} 45^{\circ} & 23' & 15'' \\ +23^{\circ} & 32' & 24'' \\ \hline \\ 68^{\circ} & 55' & 39''\end{array}\]
\(\bullet 43^{\circ}\ 25'\ 45''\ + \ 27^{\circ}\ 15'\ 23''\ \)
\[\begin{array}{rrr} 43^{\circ} & 25' & 45'' \\ +27^{\circ} & 15' & 23'' \\ \hline \\ 70^{\circ} & 40' & 68'' \\ & +1' & -60'' \\ \hline \\ 70^{\circ} & 41' & 8''\end{array}\]
\(\bullet 38^{\circ}\ 45'\ 15''\ + \ 49^{\circ}\ 23'\ 30''\ \)
\[\begin{array}{rrr} 38^{\circ} & 45' & 15'' \\ +49^{\circ} & 23' & 30'' \\ \hline \\ 87^{\circ} & 68' & 45'' \\ +1^{\circ} & -60' & \\ \hline \\ 88^{\circ} & 8' & 45''\end{array}\]
\(\bullet 25^{\circ}\ 53'\ 58''\ + \ 50^{\circ}\ 27'\ 23''\ \)
\[\begin{array}{rrr} 25^{\circ} & 53' & 58'' \\ +50^{\circ} & 27' & 23'' \\ \hline \\ 75^{\circ} & 80' & 81'' \\ & +1' & -60'' \\ \hline \\ 75^{\circ} & 81' & 21'' \\ +1^{\circ} & -60' & \\ \hline \\ 76^{\circ} & 21' & 21''\end{array}\]
Si tienes alguna duda, no olvides en postear.
Lo que tenemos que hacer es restar 60 a los minutos, (si es mayor de 60 el número de minutos) y sumar 1 grado. Si son los segundos los que suman más de 60 sumamos un minuto y restamos 60 segundos.
Lo vamos a ver más fácil con unos ejemplos.
\(\bullet 45^{\circ}\ 23'\ 15''\ + \ 23^{\circ}\ 32'\ 24''\ \)
\[\begin{array}{rrr} 45^{\circ} & 23' & 15'' \\ +23^{\circ} & 32' & 24'' \\ \hline \\ 68^{\circ} & 55' & 39''\end{array}\]
\(\bullet 43^{\circ}\ 25'\ 45''\ + \ 27^{\circ}\ 15'\ 23''\ \)
\[\begin{array}{rrr} 43^{\circ} & 25' & 45'' \\ +27^{\circ} & 15' & 23'' \\ \hline \\ 70^{\circ} & 40' & 68'' \\ & +1' & -60'' \\ \hline \\ 70^{\circ} & 41' & 8''\end{array}\]
\(\bullet 38^{\circ}\ 45'\ 15''\ + \ 49^{\circ}\ 23'\ 30''\ \)
\[\begin{array}{rrr} 38^{\circ} & 45' & 15'' \\ +49^{\circ} & 23' & 30'' \\ \hline \\ 87^{\circ} & 68' & 45'' \\ +1^{\circ} & -60' & \\ \hline \\ 88^{\circ} & 8' & 45''\end{array}\]
\(\bullet 25^{\circ}\ 53'\ 58''\ + \ 50^{\circ}\ 27'\ 23''\ \)
\[\begin{array}{rrr} 25^{\circ} & 53' & 58'' \\ +50^{\circ} & 27' & 23'' \\ \hline \\ 75^{\circ} & 80' & 81'' \\ & +1' & -60'' \\ \hline \\ 75^{\circ} & 81' & 21'' \\ +1^{\circ} & -60' & \\ \hline \\ 76^{\circ} & 21' & 21''\end{array}\]
Si tienes alguna duda, no olvides en postear.
Sistema sexagesimal: Pasar de forma incompleja a compleja
Para pasar de forma incompleja a compleja desde segundos. Tenemos que dividir entre 60. El resto de esa división son los segundos de la solución final.
El cociente anterior se vuelve a dividir entre 60, el resto serán los minutos de la solución final y el cociente de esta ultima división los grados de la solución final.
Con los ejercicios se verá más facil.
\(\bullet 322.345''\)
\( \ \ 322.345'':60 \rightarrow\ Cociente\ 53.372'\hspace{1cm}Resto\ 25''\ \ \)
\( \ \ 53.372':60 \rightarrow\ Cociente\ 89^{\circ}\hspace{1cm}Resto\ 32'\ \ \)
\( \ \boxed{89^{\circ}\ 32'\ 25''}\ \ \)
\(\bullet 22.550''\)
\( \ \ 22.550'':60 \rightarrow\ Cociente\ 375'\hspace{1cm}Resto\ 50''\ \ \)
\( \ \ 375':60 \rightarrow\ Cociente\ 6^{\circ}\hspace{1cm}Resto\ 15'\ \ \)
\( \ \boxed{6^{\circ}\ 15'\ 50''}\ \ \)
\(\bullet 9.210''\)
\( \ \ 9.210'':60 \rightarrow\ Cociente\ 153'\hspace{1cm}Resto\ 30''\ \ \)
\( \ \ 153':60 \rightarrow\ Cociente\ 2^{\circ}\hspace{1cm}Resto\ 33'\ \ \)
\( \ \boxed{2^{\circ}\ 33'\ 30''}\ \ \)
\(\bullet 48.935''\)
\( \ \ 48.935'':60 \rightarrow\ Cociente\ 815'\hspace{1cm}Resto\ 35''\ \ \)
\( \ \ 815':60 \rightarrow\ Cociente\ 13^{\circ}\hspace{1cm}Resto\ 35'\ \ \)
\( \ \boxed{13^{\circ}\ 35'\ 35''}\ \ \)
Para saber si la solución es correcta pasamos de compleja a incompleja y nos tiene que dar de resultado el enunciado.
Si tenéis alguna duda, ya sabéis poned un mensaje en los comentarios.
El cociente anterior se vuelve a dividir entre 60, el resto serán los minutos de la solución final y el cociente de esta ultima división los grados de la solución final.
Con los ejercicios se verá más facil.
\(\bullet 322.345''\)
\( \ \ 322.345'':60 \rightarrow\ Cociente\ 53.372'\hspace{1cm}Resto\ 25''\ \ \)
\( \ \ 53.372':60 \rightarrow\ Cociente\ 89^{\circ}\hspace{1cm}Resto\ 32'\ \ \)
\( \ \boxed{89^{\circ}\ 32'\ 25''}\ \ \)
\(\bullet 22.550''\)
\( \ \ 22.550'':60 \rightarrow\ Cociente\ 375'\hspace{1cm}Resto\ 50''\ \ \)
\( \ \ 375':60 \rightarrow\ Cociente\ 6^{\circ}\hspace{1cm}Resto\ 15'\ \ \)
\( \ \boxed{6^{\circ}\ 15'\ 50''}\ \ \)
\(\bullet 9.210''\)
\( \ \ 9.210'':60 \rightarrow\ Cociente\ 153'\hspace{1cm}Resto\ 30''\ \ \)
\( \ \ 153':60 \rightarrow\ Cociente\ 2^{\circ}\hspace{1cm}Resto\ 33'\ \ \)
\( \ \boxed{2^{\circ}\ 33'\ 30''}\ \ \)
\(\bullet 48.935''\)
\( \ \ 48.935'':60 \rightarrow\ Cociente\ 815'\hspace{1cm}Resto\ 35''\ \ \)
\( \ \ 815':60 \rightarrow\ Cociente\ 13^{\circ}\hspace{1cm}Resto\ 35'\ \ \)
\( \ \boxed{13^{\circ}\ 35'\ 35''}\ \ \)
Para saber si la solución es correcta pasamos de compleja a incompleja y nos tiene que dar de resultado el enunciado.
Si tenéis alguna duda, ya sabéis poned un mensaje en los comentarios.
Sistema sexagesimal: Pasar de forma compleja a incompleja
El sistema sexagesimal se usa tanto en medida de ángulos como de tiempo:
Ejemplos: \(2 h\ 3 min \ 53 s\hspace{2cm}42^{\circ}\ 23'\ 45''\)
Para pasar de una unidad a otra se multiplica o divide por 60 (sexagesimal)
Ejemplos: \(1h = 60 min = 3600 s\hspace{2cm}1^{\circ} = 60' = 3600''\)
Una medida de tiempo o ángulo en forma compleja se encuentra en varias unidades.
Ejemplos: \(2 h\ 3 min \ 53 s\hspace{2cm}42^{\circ}\ 23'\ 45''\)
Si queremos pasarlas a incompleja la transformamos a una sola unidad (grados,horas, minutos o segundos).
Pasar estos ángulos de forma compleja a incompleja en segundos.
\(\bullet\ 36^{\circ}\ 0'\ 13''\)
\[\begin{array}{rcr} 36^{\circ}\dfrac {60'} {1^{\circ}}\cdot \dfrac {60''} {1'} & = & 129.600'' \\ 0'\cdot \dfrac {60''} {1'} & = & 0'' \\ 13'' & = & + 13'' \\ \hline \\ 36^{\circ}\ 0'\ 13'' & = & 129.613'' \end{array}\]
\(\bullet\ 25^{\circ}\ 50'\ 0 ''\)
\[\begin{array}{rcr} 25^{\circ}\dfrac {60'} {1^{\circ}}\cdot \dfrac {60''} {1'} & = & 90.000'' \\ 50'\cdot \dfrac {60''} {1'} & = & 3.000'' \\ 0'' & = & + 0'' \\ \hline \\ 25^{\circ}\ 50'\ 0'' & = & 93.000'' \end{array}\]
\(\bullet\ 21^{\circ}\ 23'\ 45''\)
\[\begin{array}{rcr} 21^{\circ}\dfrac {60'} {1^{\circ}}\cdot \dfrac {60''} {1'} & = & 75.600'' \\ 23'\cdot \dfrac {60''} {1'} & = & 1.380'' \\ 45'' & = & + 45'' \\ \hline \\ 21^{\circ}\ 23'\ 45'' & = & 77.025'' \end{array}\]
\(\bullet\ 45^{\circ}\ 40'\ 22''\)
\[\begin{array}{rcr} 45^{\circ}\dfrac {60'} {1^{\circ}}\cdot \dfrac {60''} {1'} & = & 162.000'' \\ 40'\cdot \dfrac {60''} {1'} & = & 2.400'' \\ 22'' & = & + 22'' \\ \hline \\ 45^{\circ}\ 40'\ 22'' & = & 164.422'' \end{array}\]
\(\bullet\ 125^{\circ}\ 15'\ 10''\)
\[\begin{array}{rcr} 125^{\circ}\dfrac {60'} {1^{\circ}}\cdot \dfrac {60''} {1'} & = & 450.000'' \\ 15'\cdot \dfrac {60''} {1'} & = & 900'' \\ 10'' & = & + 10'' \\ \hline \\ 125^{\circ}\ 15'\ 10'' & = & 450.910'' \end{array}\]
Si tenéis alguna duda, haced un comentario. Muchas gracias.
miércoles, 26 de febrero de 2014
Ecuaciones de primer grado
Son aquellas ecuaciones cuya incógnita es de grado 1, no están elevadas al cuadrado, al cubo, etc.
Ejemplo: \(x-3=0\) el valor de \(x\) para que se cumpla la igualdad es \(x=3\)
Cuando pasamos un termino que está sumando o restando a la otra parte de la igualdad se le cambia su signo. Intentamos agrupar monomios semejantes (en este caso los que llevan x) y los que no llevan a cada lado de la igualdad
Ejemplo: \(5x-3=2\rightarrow 5x=2+3\)
Para hallar la \(x\) pasamos su coeficiente al otro lado de la igualdad, si esta multiplicando dividiendo y viceversa
Ejemplo: \(3x=6\rightarrow x=\dfrac {6} {3}=2\)
Para comprobar si el ejercicio está bien resulto sustituimos la \(x\) por la solución.
Aquí os muestro 5 ecuaciones de primer grado resueltas:
\(\bullet 4x-6=-4x+18\)
\(\ \ 4x+4x=18+6\\\)
\(\ \ 8x=24\\\)
\(\ \ x=\dfrac {24} {8}=3\\\)
\(\ \ \boxed{x=3}\\\)
\(\bullet -5x+4=-2x-8\)
\(\ \ -5x+2x=-8-4\\\)
\(\ \ -3x=-12\\\)
\(\ \ x=\dfrac {-12} {-3}=4\\\)
\(\ \ \boxed{x=4}\\\)
\(\bullet 4-3\left( 2x-1\right) =-2\\\)
\(\ \ 4-6x+3=-2\\\)
\(\ \ -6x=-2-4-3\\\)
\(\ \ -6x=-9\\\)
\(\ \ x=\dfrac {-9} {-6}=\dfrac {3} {2}\\\)
\(\ \ \boxed{x=\dfrac {3} {2}}\\\)
\(\bullet 3x+4\left( 2 -2x\right) =3\left( x-8\right)\)
\(\ \ 3x+8-8x=3x-24\\\)
\(\ \ 3x+8-8x=3x-24\\\)
\(\ \ -8x=-32\\\)
\(\ \ x=\dfrac {-32} {-8}=4\\\)
\(\ \ \boxed{x=4}\\\)
\(\bullet \dfrac {x+3} {5}+\dfrac {x-32} {10}=-2\)
\(\ \ \dfrac {2x+6+x-32} {10}=-2\\\)
\(\ \ \dfrac {3x-26} {10}=-2\\\)
\(\ \ 3x-26=-20\\\)
\(\ \ x=\dfrac {-20+26} {3}=\dfrac {6} {3}=2\\\)
\(\ \ \boxed{x=2}\\\)
Ejemplo: \(x-3=0\) el valor de \(x\) para que se cumpla la igualdad es \(x=3\)
Cuando pasamos un termino que está sumando o restando a la otra parte de la igualdad se le cambia su signo. Intentamos agrupar monomios semejantes (en este caso los que llevan x) y los que no llevan a cada lado de la igualdad
Ejemplo: \(5x-3=2\rightarrow 5x=2+3\)
Para hallar la \(x\) pasamos su coeficiente al otro lado de la igualdad, si esta multiplicando dividiendo y viceversa
Ejemplo: \(3x=6\rightarrow x=\dfrac {6} {3}=2\)
Para comprobar si el ejercicio está bien resulto sustituimos la \(x\) por la solución.
Aquí os muestro 5 ecuaciones de primer grado resueltas:
\(\bullet 4x-6=-4x+18\)
\(\ \ 4x+4x=18+6\\\)
\(\ \ 8x=24\\\)
\(\ \ x=\dfrac {24} {8}=3\\\)
\(\ \ \boxed{x=3}\\\)
\(\bullet -5x+4=-2x-8\)
\(\ \ -5x+2x=-8-4\\\)
\(\ \ -3x=-12\\\)
\(\ \ x=\dfrac {-12} {-3}=4\\\)
\(\ \ \boxed{x=4}\\\)
\(\bullet 4-3\left( 2x-1\right) =-2\\\)
\(\ \ 4-6x+3=-2\\\)
\(\ \ -6x=-2-4-3\\\)
\(\ \ -6x=-9\\\)
\(\ \ x=\dfrac {-9} {-6}=\dfrac {3} {2}\\\)
\(\ \ \boxed{x=\dfrac {3} {2}}\\\)
\(\bullet 3x+4\left( 2 -2x\right) =3\left( x-8\right)\)
\(\ \ 3x+8-8x=3x-24\\\)
\(\ \ 3x+8-8x=3x-24\\\)
\(\ \ -8x=-32\\\)
\(\ \ x=\dfrac {-32} {-8}=4\\\)
\(\ \ \boxed{x=4}\\\)
\(\bullet \dfrac {x+3} {5}+\dfrac {x-32} {10}=-2\)
\(\ \ \dfrac {2x+6+x-32} {10}=-2\\\)
\(\ \ \dfrac {3x-26} {10}=-2\\\)
\(\ \ 3x-26=-20\\\)
\(\ \ x=\dfrac {-20+26} {3}=\dfrac {6} {3}=2\\\)
\(\ \ \boxed{x=2}\\\)
Sacar factor común de un polinomio (sencillo)
El factor común de un polinomio, tendrá de coeficiente el M.C.D (Máximo Común Divisor) de los coeficientes de los monomios y de la parte literal el menor de los exponentes de cada variable (si hay varias). Para saber si es correcto el ejercicio deberemos realizar el producto de la solución y que sea igual al enunciado.
Os dejo cinco ejercicios para sacar el factor común de unos polinomios.
\(\bullet 5x^{3}-10x^{2}+15x-20=5\left( x^{3}-2x^{2}+3x-4\right) \)
\(\bullet x^{2}y+3xy+4y=y\left( x^{2}+3x+4\right)\)
\(\bullet 3a+9b-27c=3\left( a+3b-9c\right) \)
\(\bullet 7a^{11}b^{9}+3a^{8}b^{7}-5a^{9}b^{6}=a^{8}b^{6}\left( 7a^{3}b^{3}+3b-5a\right) \)
\(\bullet 4a^{2}b^{3}c^{2}-2ab^{2}c+6a^{3}b^{4}c^{5}=2ab^{2}c\left( 2abc-1-3a^{2}b^{2}c^{4}\right) \)
Si tenéis alguna pregunta o algún ejercicio que no sepáis hacer escribirme un mensaje en los comentarios y os resolveré las dudas.
Os dejo cinco ejercicios para sacar el factor común de unos polinomios.
\(\bullet 5x^{3}-10x^{2}+15x-20=5\left( x^{3}-2x^{2}+3x-4\right) \)
\(\bullet x^{2}y+3xy+4y=y\left( x^{2}+3x+4\right)\)
\(\bullet 3a+9b-27c=3\left( a+3b-9c\right) \)
\(\bullet 7a^{11}b^{9}+3a^{8}b^{7}-5a^{9}b^{6}=a^{8}b^{6}\left( 7a^{3}b^{3}+3b-5a\right) \)
\(\bullet 4a^{2}b^{3}c^{2}-2ab^{2}c+6a^{3}b^{4}c^{5}=2ab^{2}c\left( 2abc-1-3a^{2}b^{2}c^{4}\right) \)
Si tenéis alguna pregunta o algún ejercicio que no sepáis hacer escribirme un mensaje en los comentarios y os resolveré las dudas.
Multiplicación de polinomios
Se multiplicaran entre sí cada miembro de los polinomios y se sumaran monomios semejantes. Aquí tenéis cinco ejercicios resueltos de multiplicación de monomios.
\(\bullet 5x\left( x-2\right) =\boxed{10x^{2}-10x}\)
\(\bullet\left( 3x-2\right) \left( x+3\right) =3x^{2}+9x-2x-6=\boxed{3x^{2}+7x-6}\)
\(\bullet\left( x-2\right) \left( 4x^{2}+6x-3\right) =4x^{3}+6x^{2}-3x-8x^{2}-12x+6=\)
\(=\boxed{4x^{3}-2x^{2}-15x+6}\)
\(\bullet\left( x+3\right) ^{2}=\left( x+3\right) \left( x+3\right) =x^{2}+3x+3x+9=\boxed{x^{2}+6x+9}\)
\(\bullet 2xy\left( 4x^{2}y-4y\right) =8x^{2+1}y^{1+1}-8xy^{1+1}=\boxed{8x^{3}y^{2}-8xy^{2}}\)
Si tenéis alguna pregunta, no dudéis en postear un comentario
\(\bullet 5x\left( x-2\right) =\boxed{10x^{2}-10x}\)
\(\bullet\left( 3x-2\right) \left( x+3\right) =3x^{2}+9x-2x-6=\boxed{3x^{2}+7x-6}\)
\(\bullet\left( x-2\right) \left( 4x^{2}+6x-3\right) =4x^{3}+6x^{2}-3x-8x^{2}-12x+6=\)
\(=\boxed{4x^{3}-2x^{2}-15x+6}\)
\(\bullet\left( x+3\right) ^{2}=\left( x+3\right) \left( x+3\right) =x^{2}+3x+3x+9=\boxed{x^{2}+6x+9}\)
\(\bullet 2xy\left( 4x^{2}y-4y\right) =8x^{2+1}y^{1+1}-8xy^{1+1}=\boxed{8x^{3}y^{2}-8xy^{2}}\)
Si tenéis alguna pregunta, no dudéis en postear un comentario
martes, 25 de febrero de 2014
Valor numérico de polinomios
En los siguientes ejercicios vamos a calcular el valor numérico de los siguientes polinomios.
\(\bullet\ P\left( x\right) =3x^{2}-5x^{4}+3x\ \ cuando \ \ x=1\)
\( \ \ P\left( 1\right) =3\cdot 1-5\cdot 1+3\cdot 1=\boxed{1}\\\)
\(\bullet\ Q\left( x\right) =x^{4}-x^{2}+9x\ \ cuando \ \ x=-1\)
\( \ \ Q\left( -1\right) =1-1-9=\boxed{-9}\\\)
\(\bullet\ R\left( x\right) =x^{2}-3x+4\ \ cuando \ \ x=2\)
\( \ \ R\left( 2\right) =2^{2}-3\cdot 2+4=\boxed2\\\)
\(\bullet\ S\left( x\right) =3x^{2}+4x-2\ \ cuando \ \ x=-2\)
\( \ \ S\left( -2\right) =3\cdot 2^{2}-4\cdot 2-2=12-8-2=\boxed2\\\)
\(\bullet\ T\left( x\right) =4x^{2}-3x^{5}-x^{3}+3\ \ cuando \ \ x=-2\)
\( \ \ T\left( -2\right) =4\cdot 2^{2}-\left( -3\cdot2^{5}\right) -\left( -2\right) ^{3}+3=16+96+8+3=\boxed{123}\\\)
\(\bullet\ P\left( x\right) =3x^{2}-5x^{4}+3x\ \ cuando \ \ x=1\)
\( \ \ P\left( 1\right) =3\cdot 1-5\cdot 1+3\cdot 1=\boxed{1}\\\)
\(\bullet\ Q\left( x\right) =x^{4}-x^{2}+9x\ \ cuando \ \ x=-1\)
\( \ \ Q\left( -1\right) =1-1-9=\boxed{-9}\\\)
\(\bullet\ R\left( x\right) =x^{2}-3x+4\ \ cuando \ \ x=2\)
\( \ \ R\left( 2\right) =2^{2}-3\cdot 2+4=\boxed2\\\)
\(\bullet\ S\left( x\right) =3x^{2}+4x-2\ \ cuando \ \ x=-2\)
\( \ \ S\left( -2\right) =3\cdot 2^{2}-4\cdot 2-2=12-8-2=\boxed2\\\)
\(\bullet\ T\left( x\right) =4x^{2}-3x^{5}-x^{3}+3\ \ cuando \ \ x=-2\)
\( \ \ T\left( -2\right) =4\cdot 2^{2}-\left( -3\cdot2^{5}\right) -\left( -2\right) ^{3}+3=16+96+8+3=\boxed{123}\\\)
Suma y resta de polinomios
Aquí os dejo ejercicios de sumas de polinomios
\(\ \ \ \ P\left( x\right) +Q\left( x\right)=x^{2}-3x+4+3x^{2}+4x-2=\boxed{4x^{2}+x+2}\\\\\)
\(\ \ \ \ P\left( x\right) -Q\left( x\right)=x^{2}-3x+4-\left( 3x^{2}+4x-2\right)=\\\\\)
\(\ \ \ \ =x^{2}-3x+4-3x^{2}-4x+2=\boxed{-2x^{2}-7x+6}\\\\\)
\(\ \ \ \ P\left( x\right) +Q\left( x\right)=4x^{2}-3x^{5}-x^{3}+3-x^{3}+4-5x^{2}=\boxed{-3x^{5}-2x^{3}-x^{2}+7}\\\\\)
\(\ \ \ \ P\left( x\right) -Q\left( x\right)=4x^{2}-3x^{5}-x^{3}+3-\left( -x^{3}+4-5x^{2}\right) =\\\\\)
\(\ \ \ \ =4x^{2}-3x^{5}-x^{3}+3+x^{3}-4+5x^{2}=\boxed{-3x^{5}+9x^{2}-1}\\\\\)
\(\bullet\left( 3x^{2}-5x^{4}+3x\right) +\left( x^{4}-x^{2}+9x\right) =\)
\(=\left( -5+1\right) x^{4}+\left( 3-1\right) x^{2}+\left( 3+9\right) x=\)
\(=\boxed{-4x^{4}+2x^{2}+12x}\)
\(\bullet\) Siendo \(P\left( x\right) =x^{2}-3x+4\ \ ; \ \ Q\left( x\right) =3x^{2}+4x-2\) hallar:
\(\ \ P\left( x\right) +Q\left( x\right)\ \ y \ \ P\left( x\right) -Q\left( x\right)\\\)
\(\ \ \ \ P\left( x\right) +Q\left( x\right)=x^{2}-3x+4+3x^{2}+4x-2=\boxed{4x^{2}+x+2}\\\\\)
\(\ \ \ \ P\left( x\right) -Q\left( x\right)=x^{2}-3x+4-\left( 3x^{2}+4x-2\right)=\\\\\)
\(\ \ \ \ =x^{2}-3x+4-3x^{2}-4x+2=\boxed{-2x^{2}-7x+6}\\\\\)
\(\bullet\) Siendo \(P\left( x\right) =4x^{2}-3x^{5}-x^{3}+3\ \ ; \ \ Q\left( x\right) =-x^{3}+4-5x^{2}\) hallar:
\(\ \ P\left( x\right) +Q\left( x\right)\ \ y \ \ P\left( x\right) -Q\left( x\right)\\\)
\(\ \ \ \ P\left( x\right) +Q\left( x\right)=4x^{2}-3x^{5}-x^{3}+3-x^{3}+4-5x^{2}=\boxed{-3x^{5}-2x^{3}-x^{2}+7}\\\\\)
\(\ \ \ \ P\left( x\right) -Q\left( x\right)=4x^{2}-3x^{5}-x^{3}+3-\left( -x^{3}+4-5x^{2}\right) =\\\\\)
\(\ \ \ \ =4x^{2}-3x^{5}-x^{3}+3+x^{3}-4+5x^{2}=\boxed{-3x^{5}+9x^{2}-1}\\\\\)
Lenguaje algebraico
Vamos a explicar en esta entrada diferentes términos utilizados en el lenguaje algebraico.
Monomio: Es el producto de un valor conocido (coeficiente) y de uno o varios valores desconocidos (parte literal):
Ejemplo: \( -5xz^{2}\) donde -5 es el coeficiente, y \(xz^{2}\) es la parte literal.
Monomios semejantes: Son aquellos monomios con la misma parte literal.
Ejemplo: \(3xz^{2}\) y \(-5xz^{2}\)
Suma y resta de monomios: Sólo se pueden realizar si dos monomios son semejantes.
Ejemplo: \(3xz^{2}-5xz^{2}=-2xz^{2}\)
Producto y cociente de monomios: Se realiza los coeficientes por un lado, y en la parte literal cada parte variable con la suya.
Ejemplo: \(3xz^{2}\cdot 5xz^{2}=-15x^{1+1}z^{2+2}\)=\-15x^{2}z^{4}
Polinomio: Suma o resta de varios monomios
\(P\left( x\right) =5x^{3}-3x^{2}+5x\)
Valor numérico: Se sustituye la variable por un determinado valor.
\(P\left( x\right) =5x^{3}-3x^{2}+5x\) \(x=3\)
\(5\cdot 27-3\cdot 9+5\cdot 3=123\)
Factor común: Convertir ciertas sumas en producto
\(P\left( x\right) =5x^{3}-3x^{2}+5x= x\left( 5x^{2}-3x+5\right) \)
Monomio: Es el producto de un valor conocido (coeficiente) y de uno o varios valores desconocidos (parte literal):
Ejemplo: \( -5xz^{2}\) donde -5 es el coeficiente, y \(xz^{2}\) es la parte literal.
Monomios semejantes: Son aquellos monomios con la misma parte literal.
Ejemplo: \(3xz^{2}\) y \(-5xz^{2}\)
Suma y resta de monomios: Sólo se pueden realizar si dos monomios son semejantes.
Ejemplo: \(3xz^{2}-5xz^{2}=-2xz^{2}\)
Producto y cociente de monomios: Se realiza los coeficientes por un lado, y en la parte literal cada parte variable con la suya.
Ejemplo: \(3xz^{2}\cdot 5xz^{2}=-15x^{1+1}z^{2+2}\)=\-15x^{2}z^{4}
Polinomio: Suma o resta de varios monomios
\(P\left( x\right) =5x^{3}-3x^{2}+5x\)
Valor numérico: Se sustituye la variable por un determinado valor.
\(P\left( x\right) =5x^{3}-3x^{2}+5x\) \(x=3\)
\(5\cdot 27-3\cdot 9+5\cdot 3=123\)
Factor común: Convertir ciertas sumas en producto
\(P\left( x\right) =5x^{3}-3x^{2}+5x= x\left( 5x^{2}-3x+5\right) \)
Operaciones combinadas con decimales
Estos ejercicios son un resumen de lo visto anteriormente. Potencias, parentesis, fracciones, números decimales, etc. Os recuerdo que no dudéis en postear si tenéis alguna duda de matemáticas os la resolveré en cualquier momento.
\(\bullet 0,72\cdot 0,3\cdot 10^{3}-2,327= \dfrac {72} {100}\cdot \dfrac {3} {10}.10^{3}-2,327=216-2,327=\boxed{213,673}\)
\(\bullet 10^{3}\cdot 0,05-70\cdot 0,7+3,1\cdot \left( -0,72\right) =10^{3}\cdot \dfrac {5} {10^{2}}-70\cdot \dfrac {7} {10}-3,1.0,72=\)
\(=50-49-2,232=\boxed{-1,232}\)
\(\bullet 2,5\cdot 10^{-2}+3\cdot 10^{3}-2,5=\dfrac {25} {1000}+3\cdot 10^{3}-2,5=\boxed{2997,525}\)
\(\bullet 9,85\cdot \left( -1,4\right) +2,32\cdot 3,50-16,7\cdot \left( -0,1\right)= -13,79+8,12+1,67=\boxed{-4}\)
\(\bullet 0,72\cdot 0,3\cdot 10^{3}-2,327= \dfrac {72} {100}\cdot \dfrac {3} {10}.10^{3}-2,327=216-2,327=\boxed{213,673}\)
\(\bullet 10^{3}\cdot 0,05-70\cdot 0,7+3,1\cdot \left( -0,72\right) =10^{3}\cdot \dfrac {5} {10^{2}}-70\cdot \dfrac {7} {10}-3,1.0,72=\)
\(=50-49-2,232=\boxed{-1,232}\)
\(\bullet 2,5\cdot 10^{-2}+3\cdot 10^{3}-2,5=\dfrac {25} {1000}+3\cdot 10^{3}-2,5=\boxed{2997,525}\)
\(\bullet 9,85\cdot \left( -1,4\right) +2,32\cdot 3,50-16,7\cdot \left( -0,1\right)= -13,79+8,12+1,67=\boxed{-4}\)
lunes, 24 de febrero de 2014
Conversión de número decimal periódico mixto a fracción
Un número decimal periódico mixto, es aquel número decimal que tiene anteperiodo (cifras decimales que
no se repiten) y cifras decimales que se repiten hasta el infinito. Ejemplo: \(5,31\widehat{23}=5,3123232323\ldots \)
Para convertirlo en fracción el numerador es igual a la diferencia entre todo el numero sin coma y y el
número que forman la parte entera y el anteperiodo.
Os dejo nuevos ejercicios aquí, si tenéis alguna sugerencia, duda sobre éste o cualquier ejercicio de la web
poned un comentario, lo resolveré con mucho gusto.
\(\bullet 0,00\widehat{2}=\dfrac {2-0} {900}=\dfrac {2} {900}=\boxed{\dfrac {1} {450}}\)
\(\bullet 1,4\widehat{5}=\dfrac {145-14} {90}=\boxed{\dfrac {131} {90}}\)
\(\bullet 3,2\widehat{31}=\dfrac {3231-32} {990}=\boxed{\dfrac {3199} {990}}\)
\(\bullet 35,2\widehat{3}=\dfrac {3523-352} {90}=\dfrac {3171} {90}=\boxed{\dfrac {1057} {30}}\)
\(\bullet 5,78\widehat{83}=\dfrac {57883-578} {9900}=\dfrac {57305} {9900}=\boxed{\dfrac {11461} {1980}}\)
no se repiten) y cifras decimales que se repiten hasta el infinito. Ejemplo: \(5,31\widehat{23}=5,3123232323\ldots \)
Para convertirlo en fracción el numerador es igual a la diferencia entre todo el numero sin coma y y el
número que forman la parte entera y el anteperiodo.
Os dejo nuevos ejercicios aquí, si tenéis alguna sugerencia, duda sobre éste o cualquier ejercicio de la web
poned un comentario, lo resolveré con mucho gusto.
\(\bullet 0,00\widehat{2}=\dfrac {2-0} {900}=\dfrac {2} {900}=\boxed{\dfrac {1} {450}}\)
\(\bullet 1,4\widehat{5}=\dfrac {145-14} {90}=\boxed{\dfrac {131} {90}}\)
\(\bullet 3,2\widehat{31}=\dfrac {3231-32} {990}=\boxed{\dfrac {3199} {990}}\)
\(\bullet 35,2\widehat{3}=\dfrac {3523-352} {90}=\dfrac {3171} {90}=\boxed{\dfrac {1057} {30}}\)
\(\bullet 5,78\widehat{83}=\dfrac {57883-578} {9900}=\dfrac {57305} {9900}=\boxed{\dfrac {11461} {1980}}\)
Convertir número decimal periódico puro a fracción
Un número decimal periódico puro es aquel cuya parte decimal se repite infinitamente.
Ejemplo \(4,\widehat{3}=4,333\ldots \)
Para convertirlo en fracción, colocamos en el numerador todo el número sin la coma y le restamos la parte
entera (números a la izquierda de la coma), en el denominador colocamos tantos 9 como decimales
tengamos en el periodo \(4,\widehat{3}=\dfrac {43-4} {9}=\dfrac {34} {9}\)
\(\bullet\ 0,\widehat{3}=\dfrac {3-0} {9}=\boxed{\dfrac {1} {3}}\)
\(\bullet\ 0,\widehat{41}=\dfrac {41-0} {99}=\boxed{\dfrac {41} {99}}\)
\(\bullet\ 1,\widehat{23}=\dfrac {123-1} {99}=\boxed{\dfrac {122} {99}}\)
\(\bullet\ 3,\widehat{157}=\dfrac {3157-3} {999}=\boxed{\dfrac {3154} {999}}\)
\(\bullet\ 9,\widehat{201}=\dfrac {9201-9} {999}=\dfrac {9192} {999}=\boxed{\dfrac {3064} {333}}\)
Si tenéis alguna duda poned un comentario y os la resolveré.
Ejemplo \(4,\widehat{3}=4,333\ldots \)
Para convertirlo en fracción, colocamos en el numerador todo el número sin la coma y le restamos la parte
entera (números a la izquierda de la coma), en el denominador colocamos tantos 9 como decimales
tengamos en el periodo \(4,\widehat{3}=\dfrac {43-4} {9}=\dfrac {34} {9}\)
\(\bullet\ 0,\widehat{3}=\dfrac {3-0} {9}=\boxed{\dfrac {1} {3}}\)
\(\bullet\ 0,\widehat{41}=\dfrac {41-0} {99}=\boxed{\dfrac {41} {99}}\)
\(\bullet\ 1,\widehat{23}=\dfrac {123-1} {99}=\boxed{\dfrac {122} {99}}\)
\(\bullet\ 3,\widehat{157}=\dfrac {3157-3} {999}=\boxed{\dfrac {3154} {999}}\)
\(\bullet\ 9,\widehat{201}=\dfrac {9201-9} {999}=\dfrac {9192} {999}=\boxed{\dfrac {3064} {333}}\)
Si tenéis alguna duda poned un comentario y os la resolveré.
Convertir número decimal exacto a fracción
Son aquellos números cuya parte decimal (cifras a la derecha de la coma) tiene una cantidad finita de cifras,
Por ejemplo 15,7 tiene un solo tiene una cifra decimal.
Para convertirlo en fracción se coloca en el numerador el numero sin coma, y en el denominador un 1
seguido de tantos ceros como cifras finitas de decimales el numerador. \(15,7=\dfrac {157} {10}\)
Aquí os dejo más ejercicios, simplificad si es posible.
\(\bullet\ 74,12=\dfrac {7412} {100}=\dfrac {1853} {25}\)
\(\bullet\ 8,33=\dfrac {833} {100}\)
\(\bullet\ 0,23=\dfrac {23} {100}\)
\(\bullet\ 0,007=\dfrac {7} {1000}\)
\(\bullet\ 3,578=\dfrac {3578} {1000}=\dfrac {1789} {500}\)
Si tenéis alguna pregunta, no dudéis en poner un comentario.
Por ejemplo 15,7 tiene un solo tiene una cifra decimal.
Para convertirlo en fracción se coloca en el numerador el numero sin coma, y en el denominador un 1
seguido de tantos ceros como cifras finitas de decimales el numerador. \(15,7=\dfrac {157} {10}\)
Aquí os dejo más ejercicios, simplificad si es posible.
\(\bullet\ 74,12=\dfrac {7412} {100}=\dfrac {1853} {25}\)
\(\bullet\ 8,33=\dfrac {833} {100}\)
\(\bullet\ 0,23=\dfrac {23} {100}\)
\(\bullet\ 0,007=\dfrac {7} {1000}\)
\(\bullet\ 3,578=\dfrac {3578} {1000}=\dfrac {1789} {500}\)
Si tenéis alguna pregunta, no dudéis en poner un comentario.
domingo, 23 de febrero de 2014
Operaciones combinadas con fracciones
Os traigo unos ejercicios que combinan todo lo visto anteriormente en las fracciones.
\(\bullet3\cdot \left( \dfrac {2} {3}-\dfrac {7} {5}\right) -5\cdot \left( \dfrac {14} {21}+\dfrac {3} {9}\right)=3\cdot \left( \dfrac {2} {3}-\dfrac {7} {5}\right) -5\left( \dfrac {2} {3}+\dfrac {1} {3}\right)= \)
\(\enclose{updiagonalstrike}{3}\cdot \left( \dfrac {2\cdot 5-7\cdot 3} {\enclose{updiagonalstrike}{3}\cdot 5}\right) -5\cdot \dfrac {\enclose{updiagonalstrike}{3}} {\enclose{updiagonalstrike}{3}}=-\dfrac {11} {5}-5=\dfrac {-11-5\cdot 5} {5}=\boxed{\dfrac {-36} {5}}\)
\(\bullet\left( \dfrac {5} {2}-\dfrac {2} {3}\right) ^{2}+\dfrac {5} {12}-\dfrac {1} {9}=\left( \dfrac {5\cdot 3-2\cdot 2} {6}\right) +\dfrac {5} {12}-\dfrac {1} {9}\)
\(\left( \dfrac {11} {6}\right) ^{2}+\dfrac {5} {12}-\dfrac {1} {9}=\dfrac {121} {36}+\dfrac {5} {12}-\dfrac {1} {9}=\dfrac {121\cdot 1+5\cdot 3-1\cdot 4} {36}=\)
\(=\dfrac {132} {36}=\boxed{\dfrac {11} {3}}\)
\(\bullet\left( \dfrac {3} {5}-\dfrac {1} {2}\right) :\dfrac {3} {10}+\left( \dfrac {3} {2}+2\right) \cdot \left( 2-\dfrac {12} {7}\right) =\)
\(\left( \dfrac {3\cdot 2-1\cdot 5} {10}\right) =\dfrac {3} {10}+\left( \dfrac {3\cdot 1+2\cdot 2} {2}\right) \cdot \left( \dfrac {27-12\cdot 1} {7}\right)=\)
\(=\dfrac {1} {\enclose{updiagonalstrike}{10}}\cdot \dfrac {\enclose{updiagonalstrike}{10}} {3}+\dfrac {\enclose{updiagonalstrike}{7}} {\enclose{updiagonalstrike}{2}}\cdot \dfrac {\enclose{updiagonalstrike}{2}} {\enclose{updiagonalstrike}{7}}=\dfrac {1} {3}+1=\boxed{\dfrac {4} {3}}\)
\(\bullet\dfrac {\left( \dfrac {5} {6}+\dfrac {2} {3}\right) -\left( \dfrac {3} {2}-\dfrac {1} {4}\right) } {\left( \dfrac {3} {2}-\dfrac {4} {5}\right) -\left( \dfrac {1} {5}-\dfrac {2} {3}\right) -\dfrac {1} {2}}=\)
\(=\dfrac {\left( \dfrac {5\cdot 1+2\cdot 2} {6}\right) -\left( \dfrac {3\cdot 2-1\cdot 1} {4}\right) } {\left( \dfrac {3\cdot 5-4\cdot 2} {10}\right) -\left( \dfrac {1-3-2\cdot 5} {15}\right) -\dfrac {1} {2}}=\dfrac {\dfrac {10} {6}-\dfrac {5} {4}} {\dfrac {7} {10}-\dfrac {7} {15}-\dfrac {1} {2}}\)
\(\dfrac {\dfrac {102-15\cdot 3} {12}} {\dfrac {7\cdot 3-7\cdot 2-1\cdot 15} {30}}=\dfrac {-\dfrac {25} {12}} {-\dfrac {22} {30}}=\dfrac {25} {12}\cdot \dfrac {30} {22}=\dfrac {5^{2}\cdot\enclose{updiagonalstrike} {2}\cdot \enclose{updiagonalstrike}{3}\cdot 5} {\enclose{updiagonalstrike}{3}\cdot 2^{2}\cdot \enclose{updiagonalstrike}{2}\cdot 11}=\boxed{\dfrac {125} {44}}\)
\(\bullet3\cdot \left( \dfrac {2} {3}-\dfrac {7} {5}\right) -5\cdot \left( \dfrac {14} {21}+\dfrac {3} {9}\right)=3\cdot \left( \dfrac {2} {3}-\dfrac {7} {5}\right) -5\left( \dfrac {2} {3}+\dfrac {1} {3}\right)= \)
\(\enclose{updiagonalstrike}{3}\cdot \left( \dfrac {2\cdot 5-7\cdot 3} {\enclose{updiagonalstrike}{3}\cdot 5}\right) -5\cdot \dfrac {\enclose{updiagonalstrike}{3}} {\enclose{updiagonalstrike}{3}}=-\dfrac {11} {5}-5=\dfrac {-11-5\cdot 5} {5}=\boxed{\dfrac {-36} {5}}\)
\(\bullet\left( \dfrac {5} {2}-\dfrac {2} {3}\right) ^{2}+\dfrac {5} {12}-\dfrac {1} {9}=\left( \dfrac {5\cdot 3-2\cdot 2} {6}\right) +\dfrac {5} {12}-\dfrac {1} {9}\)
\(\left( \dfrac {11} {6}\right) ^{2}+\dfrac {5} {12}-\dfrac {1} {9}=\dfrac {121} {36}+\dfrac {5} {12}-\dfrac {1} {9}=\dfrac {121\cdot 1+5\cdot 3-1\cdot 4} {36}=\)
\(=\dfrac {132} {36}=\boxed{\dfrac {11} {3}}\)
\(\bullet\left( \dfrac {3} {5}-\dfrac {1} {2}\right) :\dfrac {3} {10}+\left( \dfrac {3} {2}+2\right) \cdot \left( 2-\dfrac {12} {7}\right) =\)
\(\left( \dfrac {3\cdot 2-1\cdot 5} {10}\right) =\dfrac {3} {10}+\left( \dfrac {3\cdot 1+2\cdot 2} {2}\right) \cdot \left( \dfrac {27-12\cdot 1} {7}\right)=\)
\(=\dfrac {1} {\enclose{updiagonalstrike}{10}}\cdot \dfrac {\enclose{updiagonalstrike}{10}} {3}+\dfrac {\enclose{updiagonalstrike}{7}} {\enclose{updiagonalstrike}{2}}\cdot \dfrac {\enclose{updiagonalstrike}{2}} {\enclose{updiagonalstrike}{7}}=\dfrac {1} {3}+1=\boxed{\dfrac {4} {3}}\)
\(\bullet\dfrac {\left( \dfrac {5} {6}+\dfrac {2} {3}\right) -\left( \dfrac {3} {2}-\dfrac {1} {4}\right) } {\left( \dfrac {3} {2}-\dfrac {4} {5}\right) -\left( \dfrac {1} {5}-\dfrac {2} {3}\right) -\dfrac {1} {2}}=\)
\(=\dfrac {\left( \dfrac {5\cdot 1+2\cdot 2} {6}\right) -\left( \dfrac {3\cdot 2-1\cdot 1} {4}\right) } {\left( \dfrac {3\cdot 5-4\cdot 2} {10}\right) -\left( \dfrac {1-3-2\cdot 5} {15}\right) -\dfrac {1} {2}}=\dfrac {\dfrac {10} {6}-\dfrac {5} {4}} {\dfrac {7} {10}-\dfrac {7} {15}-\dfrac {1} {2}}\)
\(\dfrac {\dfrac {102-15\cdot 3} {12}} {\dfrac {7\cdot 3-7\cdot 2-1\cdot 15} {30}}=\dfrac {-\dfrac {25} {12}} {-\dfrac {22} {30}}=\dfrac {25} {12}\cdot \dfrac {30} {22}=\dfrac {5^{2}\cdot\enclose{updiagonalstrike} {2}\cdot \enclose{updiagonalstrike}{3}\cdot 5} {\enclose{updiagonalstrike}{3}\cdot 2^{2}\cdot \enclose{updiagonalstrike}{2}\cdot 11}=\boxed{\dfrac {125} {44}}\)
Castillos con potencias
Para realizar estos ejercicios realizamos las operaciones del numerador y del denominador, de la fracción grande, por separado.
Unos cuentos ejemplos resueltos de "castillos con potencias".
\(\bullet\dfrac {\left( \dfrac {2} {3}\right) ^{6}\cdot \left( \dfrac {2} {3}\right) ^{7}} {\left( \dfrac {2} {3}\right) ^{3}\cdot\left( \dfrac {2} {3}\right) ^{4}\cdot \left( \dfrac {2} {3}\right) ^{5}}=\dfrac {\left( \dfrac {2} {3}\right) ^{6+7}} {\left( \dfrac {2} {3}\right) ^{3+4+5}}=\dfrac {\left( \dfrac {2} {3}\right) ^{13}} {\left( \dfrac {2} {3}\right) ^{12}}=\left( \dfrac {2} {3}\right) ^{13-12}=\boxed{\dfrac {2} {3}}\)
\(\bullet\dfrac {\left( \dfrac {1} {2}\right) ^{4}:\left( \dfrac {1} {2}\right) } {\left( \dfrac {1} {2}\right) ^{2}\dfrac {1} {2}}=\dfrac {\left( \dfrac {1} {2}\right) ^{4-1}} {\left( \dfrac {1} {2}\right) ^{2+1}}=\dfrac {\left( \dfrac {1} {2}\right) ^{3}} {\left( \dfrac {1} {2}\right) ^{3}}=\boxed{1}\)
\(\bullet\dfrac {\left[ \left( \dfrac {2} {5}\right) ^{2}\right] ^{6}\cdot\left[ \left( \dfrac {2} {5}\right) ^{9}\right] ^{4}} {\left( \dfrac {2} {5}\right) ^{40}}=\dfrac {\left( \dfrac {2} {5}\right) ^{2\cdot 6}\cdot \left( \dfrac {2} {5}\right) ^{9\cdot 4}} {\left( \dfrac {2} {5}\right) ^{40}}=\left( \dfrac {2} {5}\right) ^{26+9\cdot 4-40}=\boxed{\left( \dfrac {2} {5}\right) ^{8}}\)
Unos cuentos ejemplos resueltos de "castillos con potencias".
\(\bullet\dfrac {\left( \dfrac {2} {3}\right) ^{6}\cdot \left( \dfrac {2} {3}\right) ^{7}} {\left( \dfrac {2} {3}\right) ^{3}\cdot\left( \dfrac {2} {3}\right) ^{4}\cdot \left( \dfrac {2} {3}\right) ^{5}}=\dfrac {\left( \dfrac {2} {3}\right) ^{6+7}} {\left( \dfrac {2} {3}\right) ^{3+4+5}}=\dfrac {\left( \dfrac {2} {3}\right) ^{13}} {\left( \dfrac {2} {3}\right) ^{12}}=\left( \dfrac {2} {3}\right) ^{13-12}=\boxed{\dfrac {2} {3}}\)
\(\bullet\dfrac {\left( \dfrac {1} {2}\right) ^{4}:\left( \dfrac {1} {2}\right) } {\left( \dfrac {1} {2}\right) ^{2}\dfrac {1} {2}}=\dfrac {\left( \dfrac {1} {2}\right) ^{4-1}} {\left( \dfrac {1} {2}\right) ^{2+1}}=\dfrac {\left( \dfrac {1} {2}\right) ^{3}} {\left( \dfrac {1} {2}\right) ^{3}}=\boxed{1}\)
\(\bullet\dfrac {\left[ \left( \dfrac {2} {5}\right) ^{2}\right] ^{6}\cdot\left[ \left( \dfrac {2} {5}\right) ^{9}\right] ^{4}} {\left( \dfrac {2} {5}\right) ^{40}}=\dfrac {\left( \dfrac {2} {5}\right) ^{2\cdot 6}\cdot \left( \dfrac {2} {5}\right) ^{9\cdot 4}} {\left( \dfrac {2} {5}\right) ^{40}}=\left( \dfrac {2} {5}\right) ^{26+9\cdot 4-40}=\boxed{\left( \dfrac {2} {5}\right) ^{8}}\)
sábado, 22 de febrero de 2014
Multiplicación y división de fracciones
Para multiplicar dos fracciones, por ejemplo \(\dfrac {3} {5}\cdot \dfrac {2} {7}\) , multiplicaremos numerador por numerador, (numeros de arriba) en este caso 3 y 2, y denominador por denominador, (números de abajo) en este caso 5 y 7. Por lo tanto \(\dfrac {3} {5}\cdot{\dfrac {2} {7}}=\dfrac {6} {35}\).
Para dividir dos fracciones, por ejemplo \(\dfrac {3} {5}:\dfrac {2} {7}\), cambiamos de posición numerador y denominador de la segunda fracción y la convertimos en una multiplicación \(\dfrac {3} {5}\cdot\dfrac {7} {2}=\dfrac {21} {10}\) .
Aquí os dejo más ejercicios resueltos.
\(\bullet\dfrac {3} {5}.\dfrac {1} {3}\cdot \dfrac {2} {7}\cdot \dfrac {15} {2}=\dfrac {3\cdot 1\cdot\enclose{updiagonalstrike}{2}\cdot\enclose{updiagonalstrike}{3}\cdot\enclose{updiagonalstrike}{5}} {\enclose{updiagonalstrike}{5}\cdot\enclose{updiagonalstrike}{3}\cdot 7\cdot\enclose{updiagonalstrike}{2}}=\boxed{\dfrac {3} {7}}\)
\(\bullet\dfrac {3} {2}:\dfrac {1} {4}:\dfrac {6} {5}=\dfrac {3} {2}\cdot \dfrac {4} {1}\cdot \dfrac {5} {6}=\dfrac {\enclose{updiagonalstrike}{3}\cdot \enclose{updiagonalstrike}{2^{2}}\cdot 5} {\enclose{updiagonalstrike}{2}\cdot\enclose{updiagonalstrike}{2}\cdot\enclose{updiagonalstrike}{3}}=\boxed5\)
\(\bullet\dfrac {16} {25}:\dfrac {12} {35}=\dfrac {16} {25}\cdot \dfrac {35} {12}=\dfrac {2^{4}\cdot \enclose{updiagonalstrike}{5}\cdot 7} {5^{\enclose{updiagonalstrike}{2}}\cdot 2^{2}\cdot 3}=\dfrac {2^{2}\cdot 7} {3\cdot 5}=\boxed{\dfrac {28} {15}}\)
\(\bullet\dfrac {22} {3}\cdot \dfrac {5} {11}:\dfrac {4} {5}=\dfrac {22} {3}\cdot \dfrac {5} {11}\cdot \dfrac {5} {4}=\dfrac {\enclose{updiagonalstrike}{2}\cdot \enclose{updiagonalstrike}{11}\cdot 5\cdot 5} {3\cdot \enclose{updiagonalstrike}{11}\cdot 2^{\enclose{updiagonalstrike}{2}}}=\boxed{\dfrac {25} {6}}\)
\(\bullet\dfrac {6} {35}\cdot \dfrac {25} {9}\cdot \dfrac {12} {5}:\left( \dfrac {6} {7}\cdot \dfrac {5} {4}\right) =\dfrac {6} {35}\cdot \dfrac {25} {9}\cdot \dfrac {12} {5}:\left( \dfrac {\enclose{updiagonalstrike}{2}\cdot 3\cdot 5} {7\cdot 2^{\enclose{updiagonalstrike}{2}}}\right)\)
\(\dfrac {6} {35}\cdot \dfrac {25} {9}\cdot \dfrac {12} {5}:\dfrac {15} {14}=\dfrac {6} {35}\cdot \dfrac {25} {9}\cdot \dfrac {12} {5}\cdot \dfrac {14} {15}=\dfrac {2\cdot\enclose{updiagonalstrike} {3}\cdot\enclose{updiagonalstrike}{ 5^{2}}\cdot\enclose{updiagonalstrike}{3}\cdot 2^{2}\cdot 2\cdot \enclose{updiagonalstrike}{7}} {\enclose{updiagonalstrike}{7}\cdot 5\cdot\enclose{updiagonalstrike}{3^{2}}\cdot\enclose{updiagonalstrike} {5}\cdot\enclose{updiagonalstrike} {3}\cdot\enclose{updiagonalstrike} {5}}=\)
\(=\boxed{\dfrac {16} {15}}\)
Para dividir dos fracciones, por ejemplo \(\dfrac {3} {5}:\dfrac {2} {7}\), cambiamos de posición numerador y denominador de la segunda fracción y la convertimos en una multiplicación \(\dfrac {3} {5}\cdot\dfrac {7} {2}=\dfrac {21} {10}\) .
Aquí os dejo más ejercicios resueltos.
\(\bullet\dfrac {3} {5}.\dfrac {1} {3}\cdot \dfrac {2} {7}\cdot \dfrac {15} {2}=\dfrac {3\cdot 1\cdot\enclose{updiagonalstrike}{2}\cdot\enclose{updiagonalstrike}{3}\cdot\enclose{updiagonalstrike}{5}} {\enclose{updiagonalstrike}{5}\cdot\enclose{updiagonalstrike}{3}\cdot 7\cdot\enclose{updiagonalstrike}{2}}=\boxed{\dfrac {3} {7}}\)
\(\bullet\dfrac {3} {2}:\dfrac {1} {4}:\dfrac {6} {5}=\dfrac {3} {2}\cdot \dfrac {4} {1}\cdot \dfrac {5} {6}=\dfrac {\enclose{updiagonalstrike}{3}\cdot \enclose{updiagonalstrike}{2^{2}}\cdot 5} {\enclose{updiagonalstrike}{2}\cdot\enclose{updiagonalstrike}{2}\cdot\enclose{updiagonalstrike}{3}}=\boxed5\)
\(\bullet\dfrac {16} {25}:\dfrac {12} {35}=\dfrac {16} {25}\cdot \dfrac {35} {12}=\dfrac {2^{4}\cdot \enclose{updiagonalstrike}{5}\cdot 7} {5^{\enclose{updiagonalstrike}{2}}\cdot 2^{2}\cdot 3}=\dfrac {2^{2}\cdot 7} {3\cdot 5}=\boxed{\dfrac {28} {15}}\)
\(\bullet\dfrac {22} {3}\cdot \dfrac {5} {11}:\dfrac {4} {5}=\dfrac {22} {3}\cdot \dfrac {5} {11}\cdot \dfrac {5} {4}=\dfrac {\enclose{updiagonalstrike}{2}\cdot \enclose{updiagonalstrike}{11}\cdot 5\cdot 5} {3\cdot \enclose{updiagonalstrike}{11}\cdot 2^{\enclose{updiagonalstrike}{2}}}=\boxed{\dfrac {25} {6}}\)
\(\bullet\dfrac {6} {35}\cdot \dfrac {25} {9}\cdot \dfrac {12} {5}:\left( \dfrac {6} {7}\cdot \dfrac {5} {4}\right) =\dfrac {6} {35}\cdot \dfrac {25} {9}\cdot \dfrac {12} {5}:\left( \dfrac {\enclose{updiagonalstrike}{2}\cdot 3\cdot 5} {7\cdot 2^{\enclose{updiagonalstrike}{2}}}\right)\)
\(\dfrac {6} {35}\cdot \dfrac {25} {9}\cdot \dfrac {12} {5}:\dfrac {15} {14}=\dfrac {6} {35}\cdot \dfrac {25} {9}\cdot \dfrac {12} {5}\cdot \dfrac {14} {15}=\dfrac {2\cdot\enclose{updiagonalstrike} {3}\cdot\enclose{updiagonalstrike}{ 5^{2}}\cdot\enclose{updiagonalstrike}{3}\cdot 2^{2}\cdot 2\cdot \enclose{updiagonalstrike}{7}} {\enclose{updiagonalstrike}{7}\cdot 5\cdot\enclose{updiagonalstrike}{3^{2}}\cdot\enclose{updiagonalstrike} {5}\cdot\enclose{updiagonalstrike} {3}\cdot\enclose{updiagonalstrike} {5}}=\)
\(=\boxed{\dfrac {16} {15}}\)
viernes, 21 de febrero de 2014
Suma y resta de fracciones con distinto denominador
Para sumar o restar fracciones con distinto denominador (numero de abajo) \(\dfrac {3} {5}+\dfrac {1} {4}\) .
Tenemos que hallar el mínimo común múltiplo en este caso 20, que será el denominador de la fracción suma.
Para hallar el numerador de la fracción suma dividimos el m.c.m. entre cada denominador y el cociente por cada numerador.
\(\dfrac {3} {5}+\dfrac {1} {4}=\dfrac {3.4+15} {20}=\dfrac {12+5} {20}=\dfrac {17} {20}\)
Antes de sumar es conveniente que las fracciones estén simplificadas para facilitarnos el cálculo.
Aquí os pongo más ejemplos de sumas y restas de fracciones
\(\bullet\dfrac {4} {8}-\dfrac {16} {32}-\dfrac {6} {12}-\dfrac {14} {28}=\enclose{updiagonalstrike}{\dfrac {1} {2}}-\enclose{updiagonalstrike}{\dfrac {1} {2}}-\dfrac {1} {2}-\dfrac {1} {2}=\boxed{-1}\)
\(\bullet\dfrac {7} {12}+\dfrac {11} {18}-\dfrac {13} {24}=\dfrac {7\cdot 6+11\cdot 4-13\cdot 3} {72}=\boxed{\dfrac {47} {72}}\)
\(\bullet\dfrac {5} {20}+\dfrac {8} {64}-\dfrac {64} {128}+\dfrac {15} {30}=\dfrac {1} {4}+\dfrac {1} {8}-\enclose{updiagonalstrike}{\dfrac {1} {2}}+\enclose{updiagonalstrike}{\dfrac {1} {2}}=\dfrac {2+1} {8}=\boxed{\dfrac {3} {8}}\)
\(\bullet\dfrac {3} {4}-\dfrac {1} {3}+\dfrac {5} {9}-\dfrac {1} {2}=\dfrac {3\cdot 9-1\cdot 12+5\cdot 4-1\cdot 18} {36}=\dfrac {27-12+20-18} {36}=\)
\(=\boxed{\dfrac {17} {36}}\)
\(\bullet\dfrac {1} {4}-\dfrac {3} {5}+\dfrac {3} {4}-\dfrac {3} {10}+\dfrac {3} {20}=\dfrac {1\cdot 5-3\cdot 4+3\cdot 5-3\cdot 2+3\cdot 1} {20}=\)
\(=\dfrac {5-12+15-6+3} {20}=\dfrac {5} {20}=\boxed{\dfrac {1} {4}}\)
Tenemos que hallar el mínimo común múltiplo en este caso 20, que será el denominador de la fracción suma.
Para hallar el numerador de la fracción suma dividimos el m.c.m. entre cada denominador y el cociente por cada numerador.
\(\dfrac {3} {5}+\dfrac {1} {4}=\dfrac {3.4+15} {20}=\dfrac {12+5} {20}=\dfrac {17} {20}\)
Antes de sumar es conveniente que las fracciones estén simplificadas para facilitarnos el cálculo.
Aquí os pongo más ejemplos de sumas y restas de fracciones
\(\bullet\dfrac {4} {8}-\dfrac {16} {32}-\dfrac {6} {12}-\dfrac {14} {28}=\enclose{updiagonalstrike}{\dfrac {1} {2}}-\enclose{updiagonalstrike}{\dfrac {1} {2}}-\dfrac {1} {2}-\dfrac {1} {2}=\boxed{-1}\)
\(\bullet\dfrac {7} {12}+\dfrac {11} {18}-\dfrac {13} {24}=\dfrac {7\cdot 6+11\cdot 4-13\cdot 3} {72}=\boxed{\dfrac {47} {72}}\)
\(\bullet\dfrac {5} {20}+\dfrac {8} {64}-\dfrac {64} {128}+\dfrac {15} {30}=\dfrac {1} {4}+\dfrac {1} {8}-\enclose{updiagonalstrike}{\dfrac {1} {2}}+\enclose{updiagonalstrike}{\dfrac {1} {2}}=\dfrac {2+1} {8}=\boxed{\dfrac {3} {8}}\)
\(\bullet\dfrac {3} {4}-\dfrac {1} {3}+\dfrac {5} {9}-\dfrac {1} {2}=\dfrac {3\cdot 9-1\cdot 12+5\cdot 4-1\cdot 18} {36}=\dfrac {27-12+20-18} {36}=\)
\(=\boxed{\dfrac {17} {36}}\)
\(\bullet\dfrac {1} {4}-\dfrac {3} {5}+\dfrac {3} {4}-\dfrac {3} {10}+\dfrac {3} {20}=\dfrac {1\cdot 5-3\cdot 4+3\cdot 5-3\cdot 2+3\cdot 1} {20}=\)
\(=\dfrac {5-12+15-6+3} {20}=\dfrac {5} {20}=\boxed{\dfrac {1} {4}}\)
Mínimo común múltiplo (m.c.m.)
Para hallar el m.c.m. (Mínimo Común Múltiplo) de dos o más números, se buscan los factores comunes y no comunes con mayor exponente de esos números, por lo tanto tenemos que descomponer en factores primos, como hacíamos en el M.C.D..
Aquí os dejo unos cuantos ejercicios.
\(\bullet\ 36\;y\;45\)
\(36=\enclose{circle}[mathcolor="black"]{2^{2}}\cdot \enclose{circle}[mathcolor="black"]{3^{2}}\) \(45=3^{2}\cdot \enclose{circle}[mathcolor="black"]{5}\)
\( m.c.m. =2^{2}\cdot 3^{2}\cdot 5=\boxed{180}\)
\(\bullet\ 84\;y\;330\)
\(84=\enclose{circle}[mathcolor="black"]{2^{2}}\cdot\enclose{circle}[mathcolor="black"] {3}\cdot\enclose{circle}[mathcolor="black"] {7}\) \(330=2\cdot 3\cdot \enclose{circle}[mathcolor="black"]{5}\cdot\enclose{circle}[mathcolor="black"]{11}\)
\( m.c.m. =2^{2}\cdot 3\cdot 5\cdot 7\cdot 11=\boxed{4620}\)
\(\bullet\ 216\;y\;2450\)
\(216=\enclose{circle}[mathcolor="black"]{2^{3}}\cdot\enclose{circle}[mathcolor="black"]{3^{3}}\) \(2450=2\cdot\enclose{circle}[mathcolor="black"]{5^{2}}\cdot\enclose{circle}[mathcolor="black"]{7^{2}}\)
\( m.c.m. =2^{3}\cdot 3^{3}\cdot 5^{2}\cdot 7^{2}=\boxed{264600}\)
\(\bullet\ 64\;y\;224\)
\(64=\enclose{circle}[mathcolor="black"]{2^{6}}\) \(224=2^{5}\cdot \enclose{circle}[mathcolor="black"]{7}\)
\( m.c.m. = 2^{6}\cdot 7=\boxed{448}\)
Aquí os dejo unos cuantos ejercicios.
\(\bullet\ 36\;y\;45\)
\(36=\enclose{circle}[mathcolor="black"]{2^{2}}\cdot \enclose{circle}[mathcolor="black"]{3^{2}}\) \(45=3^{2}\cdot \enclose{circle}[mathcolor="black"]{5}\)
\( m.c.m. =2^{2}\cdot 3^{2}\cdot 5=\boxed{180}\)
\(\bullet\ 84\;y\;330\)
\(84=\enclose{circle}[mathcolor="black"]{2^{2}}\cdot\enclose{circle}[mathcolor="black"] {3}\cdot\enclose{circle}[mathcolor="black"] {7}\) \(330=2\cdot 3\cdot \enclose{circle}[mathcolor="black"]{5}\cdot\enclose{circle}[mathcolor="black"]{11}\)
\( m.c.m. =2^{2}\cdot 3\cdot 5\cdot 7\cdot 11=\boxed{4620}\)
\(\bullet\ 216\;y\;2450\)
\(216=\enclose{circle}[mathcolor="black"]{2^{3}}\cdot\enclose{circle}[mathcolor="black"]{3^{3}}\) \(2450=2\cdot\enclose{circle}[mathcolor="black"]{5^{2}}\cdot\enclose{circle}[mathcolor="black"]{7^{2}}\)
\( m.c.m. =2^{3}\cdot 3^{3}\cdot 5^{2}\cdot 7^{2}=\boxed{264600}\)
\(\bullet\ 64\;y\;224\)
\(64=\enclose{circle}[mathcolor="black"]{2^{6}}\) \(224=2^{5}\cdot \enclose{circle}[mathcolor="black"]{7}\)
\( m.c.m. = 2^{6}\cdot 7=\boxed{448}\)
Máximo Común Divisor (M.C.D.)
Para hallar el M.C.D. (Máximo Común Divisor) de dos o más números, se buscan los factores comunes con menor exponente de esos números, por lo tanto tenemos que descomponer en factores primos.
Aquí os dejo unos cuantos ejercicios.
\(\bullet\ 36\;y\;45\)
\(36=2^{2}\cdot \enclose{circle}[mathcolor="black"]{3^{2}}\) \(45=\enclose{circle}[mathcolor="black"]{{3^{2}}}\cdot 5\)
\( M.C.D = 3^{2} = \boxed9\)
\(\bullet\ 84\;y\;330\)
\(84=\enclose{circle}[mathcolor="black"]{2}^{2}\cdot \enclose{circle}[mathcolor="black"]{3}\cdot 7\) \(330=\enclose{circle}[mathcolor="black"]{2}\cdot\enclose{circle}[mathcolor="black"]{3}\cdot 5\cdot 11\)
\( M.C.D = 2\cdot 3 =\boxed6\)
\(\bullet\ 216\;y\;2450\)
\(216=\enclose{circle}[mathcolor="black"]{2}^{3}\cdot 3^{3}\) \(2450=\enclose{circle}[mathcolor="black"]{2}\cdot 5^{2}\cdot 7^{2}\)
\( M.C.D = \boxed2\)
\(\bullet\ 64\;y\;224\)
\(64=2^{6}=2\cdot \enclose{circle}[mathcolor="black"]{2^{5}}\) \(224=\enclose{circle}[mathcolor="black"]{2^{5}}\cdot 7\)
\( M.C.D = 2^{5}=\boxed{32}\)
Aquí os dejo unos cuantos ejercicios.
\(\bullet\ 36\;y\;45\)
\(36=2^{2}\cdot \enclose{circle}[mathcolor="black"]{3^{2}}\) \(45=\enclose{circle}[mathcolor="black"]{{3^{2}}}\cdot 5\)
\( M.C.D = 3^{2} = \boxed9\)
\(\bullet\ 84\;y\;330\)
\(84=\enclose{circle}[mathcolor="black"]{2}^{2}\cdot \enclose{circle}[mathcolor="black"]{3}\cdot 7\) \(330=\enclose{circle}[mathcolor="black"]{2}\cdot\enclose{circle}[mathcolor="black"]{3}\cdot 5\cdot 11\)
\( M.C.D = 2\cdot 3 =\boxed6\)
\(\bullet\ 216\;y\;2450\)
\(216=\enclose{circle}[mathcolor="black"]{2}^{3}\cdot 3^{3}\) \(2450=\enclose{circle}[mathcolor="black"]{2}\cdot 5^{2}\cdot 7^{2}\)
\( M.C.D = \boxed2\)
\(\bullet\ 64\;y\;224\)
\(64=2^{6}=2\cdot \enclose{circle}[mathcolor="black"]{2^{5}}\) \(224=\enclose{circle}[mathcolor="black"]{2^{5}}\cdot 7\)
\( M.C.D = 2^{5}=\boxed{32}\)
jueves, 20 de febrero de 2014
Descomponer y simplificar
\(\bullet\dfrac {2^{7}\cdot 2^{10}} {2^{8}\cdot 2^{5}=}\dfrac {2^{10+7}} {2^{8+5}}=2^{17-13}=\boxed{2^{4}}\)
\(\bullet\dfrac {18^{2}\cdot 150} {3^{3}\cdot 5^{2}}=\dfrac {\left( 2\cdot 3^{2}\right) ^{2}\cdot 2\cdot 3\cdot 5^{2}} {3^{3}\cdot 5^{2}}=\dfrac {2^{2}\cdot 3^{4}\cdot 2\cdot 3} {3^{3}}=2^{2+1}\cdot 3^{4+1-3}=\boxed{2^{3}\cdot 3^{2}}\)
\(\bullet\left[ \left( -2\right) ^{6}:\left( -2\right) ^{3}\right] ^{3}\cdot \left( -2\right) ^{0}\cdot \left( -2\right) ^{-4}=\left( \left( -2\right) ^{3}\right) ^{3}.\left( -2\right) ^{0}\cdot \left( -2\right) ^{-4}=\\
=\left( -2\right) ^{9}\cdot 1\cdot \left( -2\right) ^{-4}=\boxed{-2^{5}}\)
\(\bullet\dfrac {2^{10}\cdot 3^{4}\cdot 5^{6}} {65\cdot 10^{4}}=\dfrac {2^{10}\cdot 3^{4}\cdot 5^{6}} {\left( 2\cdot 3\right) ^{5}\cdot \left( 25\right) ^{4}}=\dfrac {2^{10}\cdot 3^{4}\cdot 5^{6}} {2^{5}\cdot 3^{5}\cdot 2^{4}\cdot 5^{4}}=\dfrac {2^{10}\cdot 3^{4}\cdot 5^{6}} {2^{9}\cdot 3^{5}\cdot 5^{4}}=\boxed{\dfrac {2\cdot 5^{2}} {3}}\)
\(\bullet\dfrac {36\cdot 25} {4\cdot 81}=\dfrac {{\not2^{2}}\cdot 3^{2}\cdot 5^{2}} {{\not2^{2}}\cdot 3^{4}}=\boxed{\dfrac {5^{2}} {3^{2}}}\)
\(\bullet\dfrac {18^{2}\cdot 150} {3^{3}\cdot 5^{2}}=\dfrac {\left( 2\cdot 3^{2}\right) ^{2}\cdot 2\cdot 3\cdot 5^{2}} {3^{3}\cdot 5^{2}}=\dfrac {2^{2}\cdot 3^{4}\cdot 2\cdot 3} {3^{3}}=2^{2+1}\cdot 3^{4+1-3}=\boxed{2^{3}\cdot 3^{2}}\)
\(\bullet\left[ \left( -2\right) ^{6}:\left( -2\right) ^{3}\right] ^{3}\cdot \left( -2\right) ^{0}\cdot \left( -2\right) ^{-4}=\left( \left( -2\right) ^{3}\right) ^{3}.\left( -2\right) ^{0}\cdot \left( -2\right) ^{-4}=\\
=\left( -2\right) ^{9}\cdot 1\cdot \left( -2\right) ^{-4}=\boxed{-2^{5}}\)
\(\bullet\dfrac {2^{10}\cdot 3^{4}\cdot 5^{6}} {65\cdot 10^{4}}=\dfrac {2^{10}\cdot 3^{4}\cdot 5^{6}} {\left( 2\cdot 3\right) ^{5}\cdot \left( 25\right) ^{4}}=\dfrac {2^{10}\cdot 3^{4}\cdot 5^{6}} {2^{5}\cdot 3^{5}\cdot 2^{4}\cdot 5^{4}}=\dfrac {2^{10}\cdot 3^{4}\cdot 5^{6}} {2^{9}\cdot 3^{5}\cdot 5^{4}}=\boxed{\dfrac {2\cdot 5^{2}} {3}}\)
\(\bullet\dfrac {36\cdot 25} {4\cdot 81}=\dfrac {{\not2^{2}}\cdot 3^{2}\cdot 5^{2}} {{\not2^{2}}\cdot 3^{4}}=\boxed{\dfrac {5^{2}} {3^{2}}}\)
Propiedades de las potencias
\(\bullet9\cdot 27=3^{2}\cdot 3^{3}=3^{\left( 2+3\right) }=\boxed{3^{5}}\)
\(\bullet5^{10}:\left( 5\cdot 5^{7}\right) =5^{10}:5^{8}=5^{\left( 10-8\right) }=\boxed{5^{2}}\)
\(\bullet11^{2}.9=11^{2}\cdot 3^{2}=\left( 11\cdot 3\right) ^{2}=\boxed{33^{2}}\)
\(\bullet3^{2}\left( 3^{7}\right) ^{2}=3^{2}\cdot 3^{14}=3^{\left( 2+14\right) }=\boxed{3^{16}}\)
\(\bullet5^{9}\cdot 5^{23}:5^{11}=5^{\left( 9+23-11\right) }=\boxed{5^{21}}\)
\(\bullet81:2^{4}=3^{4}:2^{4}=\boxed{\left( \dfrac {3} {2}\right) ^{4}}\)
\(\bullet5^{10}:\left( 5\cdot 5^{7}\right) =5^{10}:5^{8}=5^{\left( 10-8\right) }=\boxed{5^{2}}\)
\(\bullet11^{2}.9=11^{2}\cdot 3^{2}=\left( 11\cdot 3\right) ^{2}=\boxed{33^{2}}\)
\(\bullet3^{2}\left( 3^{7}\right) ^{2}=3^{2}\cdot 3^{14}=3^{\left( 2+14\right) }=\boxed{3^{16}}\)
\(\bullet5^{9}\cdot 5^{23}:5^{11}=5^{\left( 9+23-11\right) }=\boxed{5^{21}}\)
\(\bullet81:2^{4}=3^{4}:2^{4}=\boxed{\left( \dfrac {3} {2}\right) ^{4}}\)
miércoles, 19 de febrero de 2014
Opereaciones combinadas. Potencias y raices
Las reglas de las potencias y raíces son.
1) La base elevada a la unidad es igual a la base. Ejemplo \(2^{1}=2\)
2) La base elevada a cero es igual a la unidad. Ejemplo \(2^{0}=1\)
3) La base elevada a menos 1 es igual a la inversa de la base. Ejemplo \(2^{-1}=\dfrac {1} {2}\)
4) Multiplicación de potencias con la misma base, se deja la misma base y se suman los exponentes.
Ejemplo. \(2^{2}\cdot 2^{3}=2^{2+3}=2^{5}\)
5) División de potencias con la misma base, se deja la misma base y se restan los exponentes.
Ejemplo. \(\dfrac {2^{5}} {2^{2}}=2^{5-2}=2^{3}\).
6) Potencia de una potencia. Se deja la misma base y se multiplican los exponentes.
Ejemplo. \(\left( 2^{2}\right) ^{3}=2^{2\cdot 3}=2^{6}\)
7) La multiplicación de dos potencias con el mismo exponente pero distinta base, se deja el mismo
exponente y se multiplican las bases. Ejemplo. \(2^{3}\cdot 5^{3}=\left( 2\cdot 5\right) ^{3}=10^{3}\)
8) La división de dos potencias con el mismo exponente pero distinta base, se deja el mismo exponente yse
dividen las bases. Ejemplo. \(\dfrac {6^{4}} {2^{4}}=\left( \dfrac {6} {2}\right) ^{4}=3^{4}\).
9) Una base cuyo exponente sea negativo es igual a la inversa de la base y exponente positivo.
Ejemplo. \(2^{-5}=\dfrac {1} {2^{5}}\)
10) Una base cuyo exponente sea una fracción, es una raiz cuyo indice es el denominador del exponente y el numerador es el exponente del radicando (base).
Ejemplo. \(\left( 3\right) ^{\dfrac {2} {5}}=\sqrt [5] {3^{2}}\)
Aquí os dejo unas operaciones con potencia y raíces.
\(\bullet\left( 3^{2}\cdot 2^{2}\right) ^{0}-\sqrt {36}+\sqrt {121}=\)
\(=1-\sqrt {2^{2}\cdot 3^{2}}+\sqrt {11^{2}}=\)
\(=1-2\cdot 3+11=\)
\(=\boxed{6}\)
\(\bullet\left( -6\right) ^{3}:\left( -3\right) ^{3}+\left( -8\right) ^{2}:\left( -4\right) ^{2}=\)
\(=6^{3}:3^{3}+8^{2}:4^{2}=\)
\(=2^{3}+2^{2}=\)
\(=8+4=\)
\(=\boxed{12}\)
\(\bullet2^{-2}\cdot 2^{7}\cdot 2^{-6}\cdot 2^{4}=\)
\(=2^{7+4}\cdot 2^{-\left( 6+2\right) }=\)
\(=2^{7+4}\cdot 2^{-\left( 6+2\right) }=\)
1) La base elevada a la unidad es igual a la base. Ejemplo \(2^{1}=2\)
2) La base elevada a cero es igual a la unidad. Ejemplo \(2^{0}=1\)
3) La base elevada a menos 1 es igual a la inversa de la base. Ejemplo \(2^{-1}=\dfrac {1} {2}\)
4) Multiplicación de potencias con la misma base, se deja la misma base y se suman los exponentes.
Ejemplo. \(2^{2}\cdot 2^{3}=2^{2+3}=2^{5}\)
5) División de potencias con la misma base, se deja la misma base y se restan los exponentes.
Ejemplo. \(\dfrac {2^{5}} {2^{2}}=2^{5-2}=2^{3}\).
6) Potencia de una potencia. Se deja la misma base y se multiplican los exponentes.
Ejemplo. \(\left( 2^{2}\right) ^{3}=2^{2\cdot 3}=2^{6}\)
7) La multiplicación de dos potencias con el mismo exponente pero distinta base, se deja el mismo
exponente y se multiplican las bases. Ejemplo. \(2^{3}\cdot 5^{3}=\left( 2\cdot 5\right) ^{3}=10^{3}\)
8) La división de dos potencias con el mismo exponente pero distinta base, se deja el mismo exponente yse
dividen las bases. Ejemplo. \(\dfrac {6^{4}} {2^{4}}=\left( \dfrac {6} {2}\right) ^{4}=3^{4}\).
9) Una base cuyo exponente sea negativo es igual a la inversa de la base y exponente positivo.
Ejemplo. \(2^{-5}=\dfrac {1} {2^{5}}\)
10) Una base cuyo exponente sea una fracción, es una raiz cuyo indice es el denominador del exponente y el numerador es el exponente del radicando (base).
Ejemplo. \(\left( 3\right) ^{\dfrac {2} {5}}=\sqrt [5] {3^{2}}\)
Aquí os dejo unas operaciones con potencia y raíces.
\(\bullet\left( 3^{2}\cdot 2^{2}\right) ^{0}-\sqrt {36}+\sqrt {121}=\)
\(=1-\sqrt {2^{2}\cdot 3^{2}}+\sqrt {11^{2}}=\)
\(=1-2\cdot 3+11=\)
\(=\boxed{6}\)
\(\bullet\left( -6\right) ^{3}:\left( -3\right) ^{3}+\left( -8\right) ^{2}:\left( -4\right) ^{2}=\)
\(=6^{3}:3^{3}+8^{2}:4^{2}=\)
\(=2^{3}+2^{2}=\)
\(=8+4=\)
\(=\boxed{12}\)
\(\bullet2^{-2}\cdot 2^{7}\cdot 2^{-6}\cdot 2^{4}=\)
\(=2^{7+4}\cdot 2^{-\left( 6+2\right) }=\)
\(=2^{3}=\)
\(=\boxed{8}\)
\(\bullet\left( 5-4\right) ^{3}\cdot \left( 6-2\right) ^{0}+\sqrt [3] {5+10^{2}+20}-2\cdot \left[ 8-2\left( -2\right) ^{2}\right] =\)
\(=1^{3}\cdot 4^{0 }+\sqrt [3] {125}-2\cdot \left[ 8-2\cdot 4\right] \)
\(=1+\sqrt [3] {5^{3}}-2\cdot 0=\)
\(=1+5=\)
\(=\boxed{6}\)
\(\bullet3^{2}-\left( -4\right) ^{2}+2^{4}+\left( -2\right) ^{3}-9^{0 }+6^{1}=\)
\(=3^{2}-\left( -2^{2}\right) ^{2}+2^{4}+\left( -2\right) ^{3}-1+6=\)
\(=9-16+16-8-1+6=\)
\(=\boxed{6}\)
\(=\boxed{8}\)
\(\bullet\left( 5-4\right) ^{3}\cdot \left( 6-2\right) ^{0}+\sqrt [3] {5+10^{2}+20}-2\cdot \left[ 8-2\left( -2\right) ^{2}\right] =\)
\(=1^{3}\cdot 4^{0 }+\sqrt [3] {125}-2\cdot \left[ 8-2\cdot 4\right] \)
\(=1+\sqrt [3] {5^{3}}-2\cdot 0=\)
\(=1+5=\)
\(=\boxed{6}\)
\(\bullet3^{2}-\left( -4\right) ^{2}+2^{4}+\left( -2\right) ^{3}-9^{0 }+6^{1}=\)
\(=3^{2}-\left( -2^{2}\right) ^{2}+2^{4}+\left( -2\right) ^{3}-1+6=\)
\(=9-16+16-8-1+6=\)
\(=\boxed{6}\)
Descomposición en factores primos
Un número primo, es aquel número natural mayor que 1 y que sólo es divisible por él mismo y la unidad.
Los números primos hasta el número 20 son 2,3,5,7,11,13,17 y 19.
¿Cómo sabemos si un número es divisible por un número primo?
Aquí os dejo las reglas de divisibilidad de los primeros números primos.
Números divisibles entre 2 todos los números pares.
Ejemplos: 8,24,36
Números divisibles entre 3 los números cuyas todas cifras suman un número múltiplo de 3.
Ejemplos: 6, 21 ( 2+1=3), 54 (5+4=9) 9 múltiplo de 3
Números divisibles entre 5 los números cuya unidad acaba en 0 ó 5.
Ejemplos: 10, 35, 1000, 11115.
Números divisibles entre 7 son aquellos que eliminando la unidad y restando el doble de la unidad es un 0 ó múltiplo de 7.
Ejemplo: 371 (37-2·1=35) 35 es múltiplo de 7.
Números divisibles entre 11 son aquellos que si la diferencia de la suma de cifras de posición par e impar es 0 o múltiplo de 11.
Ejemplo: 275 Impares 2+5=7 Pares 7 Impares -Pares = 7-7 = 0.
En los números que terminan en 0 es más fácil factorizarlos como 2·5.
Aquí os dejo unos ejercicios resueltos de descomposición en factores primos.
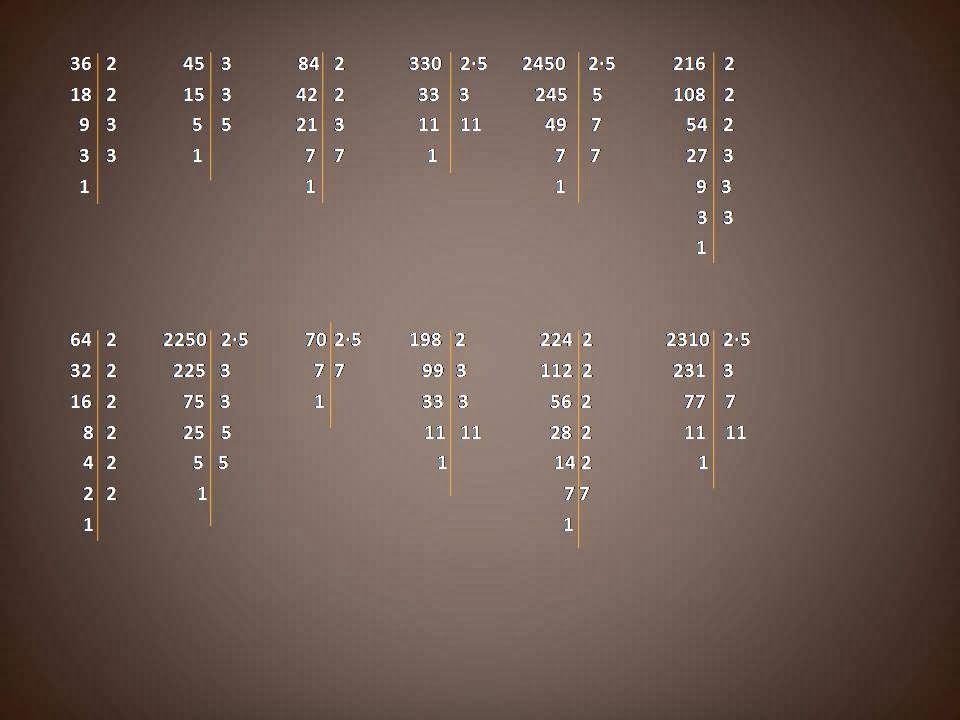height="480" width="640" />
Por lo tanto:
\(36=2^{2}\cdot 3^{2}\)
\(45=3^{2}\cdot 5\)
\(84=2^{2}\cdot 3\cdot 7\)
\(330=2\cdot 3\cdot 5\cdot 11\)
\(2450=2\cdot 5^{2}\cdot 7^{2}\)
\(216=2^{3}\cdot 3^{3}\)
\(64=2^{6}\)
\(2250=2\cdot 3^{2}\cdot 5^{3}\)
\(70=2\cdot 5\cdot 7\)
\(198=2\cdot 3^{2}\cdot 11\)
\(224=2^{5}\cdot 7\)
\(2310=2\cdot 5\cdot 3\cdot 7\cdot 11\)
Los números primos hasta el número 20 son 2,3,5,7,11,13,17 y 19.
¿Cómo sabemos si un número es divisible por un número primo?
Aquí os dejo las reglas de divisibilidad de los primeros números primos.
Números divisibles entre 2 todos los números pares.
Ejemplos: 8,24,36
Números divisibles entre 3 los números cuyas todas cifras suman un número múltiplo de 3.
Ejemplos: 6, 21 ( 2+1=3), 54 (5+4=9) 9 múltiplo de 3
Números divisibles entre 5 los números cuya unidad acaba en 0 ó 5.
Ejemplos: 10, 35, 1000, 11115.
Números divisibles entre 7 son aquellos que eliminando la unidad y restando el doble de la unidad es un 0 ó múltiplo de 7.
Ejemplo: 371 (37-2·1=35) 35 es múltiplo de 7.
Números divisibles entre 11 son aquellos que si la diferencia de la suma de cifras de posición par e impar es 0 o múltiplo de 11.
Ejemplo: 275 Impares 2+5=7 Pares 7 Impares -Pares = 7-7 = 0.
En los números que terminan en 0 es más fácil factorizarlos como 2·5.
Aquí os dejo unos ejercicios resueltos de descomposición en factores primos.
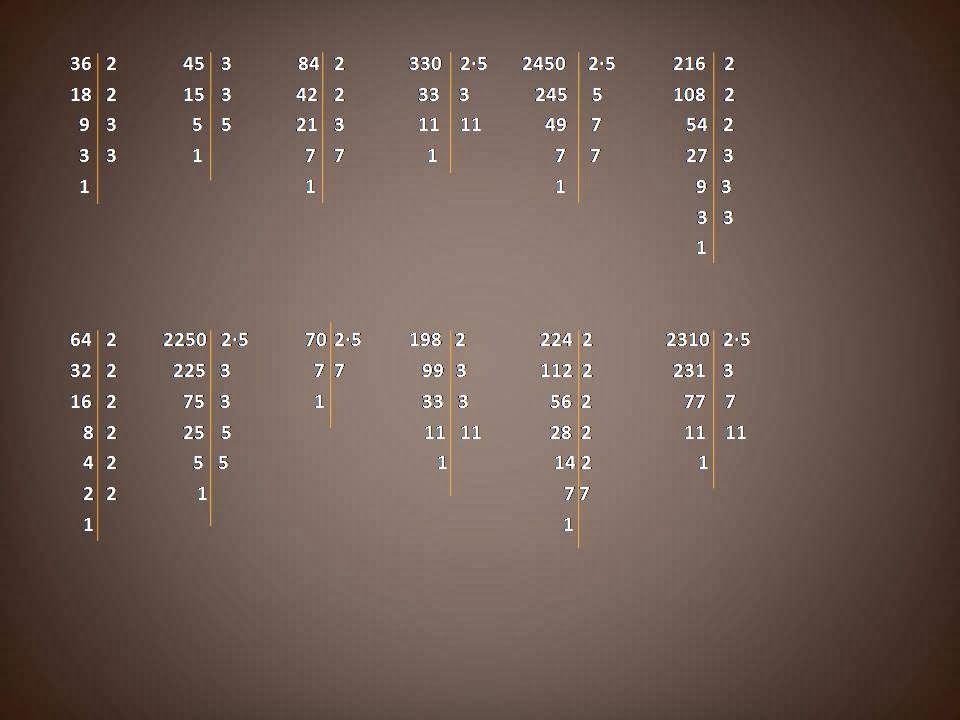height="480" width="640" />Por lo tanto:
\(36=2^{2}\cdot 3^{2}\)
\(45=3^{2}\cdot 5\)
\(84=2^{2}\cdot 3\cdot 7\)
\(330=2\cdot 3\cdot 5\cdot 11\)
\(2450=2\cdot 5^{2}\cdot 7^{2}\)
\(216=2^{3}\cdot 3^{3}\)
\(64=2^{6}\)
\(2250=2\cdot 3^{2}\cdot 5^{3}\)
\(70=2\cdot 5\cdot 7\)
\(198=2\cdot 3^{2}\cdot 11\)
\(224=2^{5}\cdot 7\)
\(2310=2\cdot 5\cdot 3\cdot 7\cdot 11\)
Operaciones combinadas (I)
Aquí os dejo unas operaciones combinadas y como se resuelven.
\(40-\left[ 5\cdot 4-3\cdot \left( 2+3\right) +5\right] \cdot 3=\)
\(=40-\left[ 5\cdot 4-3\cdot 5+5\right] \cdot 3=\)
\(=40-\left[ 20-15+5\right] \cdot 3=\)
\(=40-30\)
\(=\boxed{10}\)
\(8\cdot 5-4\cdot \left( 3+2\right) -\left( 40:8\right) \cdot 3=\)
\(=40-4\cdot 5-5\cdot 3=\)
\(=40-20-15=\)
\(=\boxed5\)
\(\left\{ -4\cdot \left( -7\right) -4\cdot \left[ 4:\left( -2\right) \right] \right\}=\)
\(=\left\{ 28-4\cdot \left[ -2\right] \right\}=\)
\(=\left\{ 28+8\right\}=\)
\(=\boxed{36}\)
\(15-9-\left( -69\right) :\left( -3\right) -\left( -17\right) +\left( -1\right)=\)
\(=15-9+69:\left( -3\right) +17-1=\)
\(=15-9-23+17-1=\)
\(=32-33=\)
\(=\boxed{-1}\)
\(\left[ -5+\left( -2\right) \cdot \left( -1\right) \right] \cdot 4+7-\left( -40\right) :\left( -4\right)=\)
\(=\left[ -5+\left( -2\right) \cdot \left( -1\right) \right] \cdot 4+7-\left( 40:4\right)=\)
\(=\left[ -5+2\right] \cdot 4+7+40:4=\)
\(=-3\cdot 4+7+40:4=\)
\(=-12+7+10=\)
\(=\boxed{-15}\)
Suscribirse a:
Entradas (Atom)
